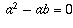Go backward to This is Not the Fallacy Go up to 1=2: A Proof using Beginning Algebra Switch to text-only version (no graphics) Go to University of Toronto Mathematics Network
Home Page
.
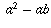However, division only makes sense when the number you are dividing by
is non-zero. In this proof,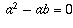 
, because we assumed
in step 1 that a=b!
Therefore, it is not legitimate to divide both sides of the equation by
,
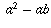because that would be division by zero, which does
not make any sense (as explained below).
In essence, this proof boils down to saying "1 times 0 equals 2 times 0, therefore 1 equals 2". The fallacy is that, just because two numbers give you the same answer (zero) after you multiply them each by zero, doesn't necessarily mean that the two numbers are the same, because anything when multiplied by zero gives zero.
This is also the reason division by zero does not make sense: there isn't
just one unambiguously determined
number q such that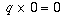 
, so
there isn't
any number that we can uniquely and unambiguously
define the quotient 0/0 to be.
If you tried to divide 1 (or some other non-zero number) by 0,
you'd run into a different problem: in this case, there is no
number q at all such that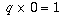 
,
so there is nothing that we can define the quotient 1/0 to be.
That's why division by zero is undefined (not just because it's a rule somebody decided on!)