Navigation Panel: 











 (These buttons explained below)
(These buttons explained below)

Answers and Explanations
More Information on Why
"Infinity" Does Exist in the Context of A Topological Space
This page provides supplementary
information to the page of explanations
on the question "does infinity exist?".
Remember, we are trying to
see why the answer is "yes" to the following question:
Does there exist some topological
space (that is, a set of objects plus a definition of what convergence means)
which,
as well as including the familiar real numbers we are used to, also includes
an "infinity" concept to which some sequences of real numbers converge?
How do we know that a topological space with these properties really exists?
Well, we just build one! Here are two ways to do it:
- Start with the real numbers, take any additional object you
like, add it to the set of real numbers, and make the resulting set
into a topological space. It turns out that all you need to do to
make a set into a topological space is come up with an appropriate
collection of subsets (which in the case of the real numbers are
unions of open intervals). It would take us too far afield to
discuss exactly why specifying an "appropriate collection of
subsets" is all it takes to completely determine all notions of
which sequences converge and which don't. However, that is in fact
all it takes, and in our new set (the real numbers together with the
additional object) there does turn out to be an appropriate
collection of subsets which makes it into a topological space, and
the resulting notion of "convergence" is such that sequences like
1, 2, 3, . . . converge to the additional object, which justifies
calling the additional object "infinity".
- If the previous construction seems too abstract, think about
drawing the real numbers on an interval of finite length, instead of
the usual infinitely long number line. (It may seem surprising that
this can be done, but all you need to do is compress the distances
so that larger numbers are drawn closer together. For instance, you
could draw the number 1 at a distance 1 from the end, 2 at a
distance 1/2 from the end, 3 at a distance 1/3 from the end, and so
on. The following picture illustrates this (not quite to scale):
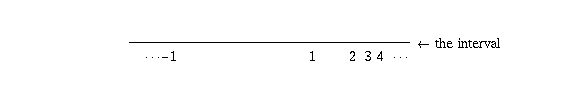
Now you can take the endpoints of the interval,
call them "infinity" and "-infinity",
and say that
a sequence of numbers 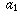 ,
, 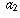 ,
, 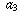 , . . .
"converges to infinity"
if and only if the dots where those numbers are drawn converge
to the right-hand endpoint
of the interval.
, . . .
"converges to infinity"
if and only if the dots where those numbers are drawn converge
to the right-hand endpoint
of the interval.
No matter which approach you take, you can define a topological space
which has the real numbers as a subset, also has an additional object
called "infinity", and in which the notion of convergence is such that
sequences like 1, 2, 3, . . . converge to this additional object. In
this sense, therefore, infinity exists.
This page last updated: September 1, 1997
Original Web Site Creator / Mathematical Content Developer:
Philip Spencer
Current Network Coordinator and Contact Person:
Any Wilk - mathnet@math.toronto.edu
Navigation Panel: 












 Go backward to Number System Context: Why Infinity Doesn't Exist
Go backward to Number System Context: Why Infinity Doesn't Exist
 Go up to Does "Infinity" Exist?
Go up to Does "Infinity" Exist?
 Go forward to Size of Sets Context: Why Infinity Does Exist
Go forward to Size of Sets Context: Why Infinity Does Exist
 Switch to text-only version (no graphics)
Switch to text-only version (no graphics)
 Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)
 Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page
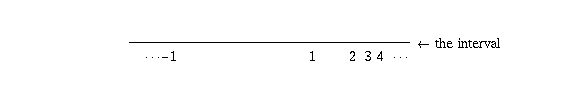
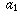 ,
, 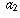 ,
, 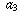 , . . .
"converges to infinity"
if and only if the dots where those numbers are drawn converge
to the right-hand endpoint
of the interval.
, . . .
"converges to infinity"
if and only if the dots where those numbers are drawn converge
to the right-hand endpoint
of the interval.
![]() Go backward to Number System Context: Why Infinity Doesn't Exist
Go backward to Number System Context: Why Infinity Doesn't Exist![]() Go up to Does "Infinity" Exist?
Go up to Does "Infinity" Exist?![]() Go forward to Size of Sets Context: Why Infinity Does Exist
Go forward to Size of Sets Context: Why Infinity Does Exist![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page