Final Exam
University of Toronto, April 29, 2005
Math 1300Y Students: Make sure to write ``1300Y'' in
the course field on the exam notebook. Solve 2 of the 3 problems in
part A and 4 of the 6 problems in part B. Each problem is worth 17
points, to a maximal total grade of 102. If you solve more than the
required 2 in 3 and 4 in 6, indicate very clearly which problems you
want graded; otherwise random ones will be left out at grading and they
may be your best ones! You have 3 hours. No outside material other than
stationary is allowed.
Math 427S Students: Make sure to write ``427S'' in the
course field on the exam notebook. Solve 5 of the 6 problems in part B,
do not solve anything in part A. Each problem is worth 20 points. If
you solve more than the required 5 in 6, indicate very clearly which
problems you want graded; otherwise random ones will be left out at
grading and they may be your best ones! You have 3 hours. No outside
material other than stationary is allowed.
Good Luck!
Part A
Problem 1. Let 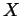 be a topological space.
be a topological space.
- Define the phrase ``
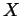 is Hausdorff''.
is Hausdorff''.
- Define the phrase ``
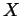 is normal''.
is normal''.
- Define the phrase ``
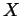 is compact''.
is compact''.
- Prove that if
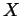 is compact and Hausdorff, it is normal.
is compact and Hausdorff, it is normal.
Problem 2. Let 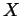 be a metric space.
be a metric space.
- Define the phrase ``
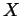 is complete''.
is complete''.
- Define the phrase ``
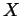 is totally bounded''.
is totally bounded''.
- Prove that if
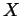 is totally bounded and complete than every sequence
in
is totally bounded and complete than every sequence
in 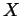 has a convergent subsequence.
has a convergent subsequence.
Problem 3.
- State the Van Kampen theorem in full.
- Let
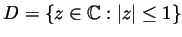 be the unit disk in the complex plane
and let
be the unit disk in the complex plane
and let 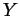 be its quotient by the relation
be its quotient by the relation
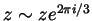 , for
, for
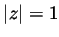 . Compute
. Compute 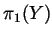 .
.
Part B
Problem 4.
- Let
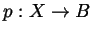 be covering map and let
be covering map and let 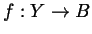 be a continuous
map. State in full the lifting theorem, which gives necessary and
sufficient conditions for the existence and uniqueness of a lift
of
be a continuous
map. State in full the lifting theorem, which gives necessary and
sufficient conditions for the existence and uniqueness of a lift
of 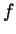 to a map
to a map
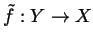 such that
such that
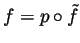 .
.
- Let
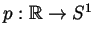 be given by
be given by
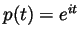 . Is it true that
every map
. Is it true that
every map
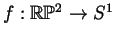 can be lifted to a map
can be lifted to a map
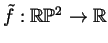 such that
such that
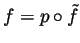 ? Justify
your answer.
? Justify
your answer.
Problem 5. Let 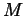 be an
be an 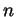 -dimensional
topological manifold (a space in which every point has a neighborhood
homeomorphic to
-dimensional
topological manifold (a space in which every point has a neighborhood
homeomorphic to
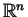 ), and let
), and let 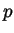 be a point in
be a point in 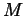 .
.
- Show that
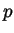 has a neighborhood
has a neighborhood 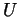 for which
for which
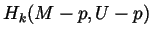 is
isomorphic to
is
isomorphic to
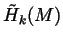 for all
for all 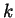 , and so that
, and so that 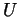 is homeomorphic
to a ball.
is homeomorphic
to a ball.
- Write the long exact sequence corresponding to the pair
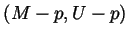 .
.
- Prove that
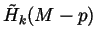 is isomorphic to
is isomorphic to
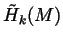 for
for 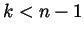 .
.
Problem 6.
- Present the space
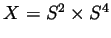 as a CW complex.
as a CW complex.
- Calculate the homology of
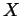 . (I.e., calculate
. (I.e., calculate 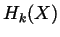 for all
for all
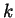 ).
).
- What is the minimal number of cells required to present
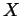 as a CW
complex? Justify your answer.
as a CW
complex? Justify your answer.
Problem 7.
- Define the degree
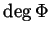 of a continuous map
of a continuous map
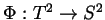 .
.
- Let
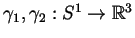 be two continuous maps such that
be two continuous maps such that
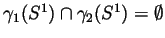 . Let
. Let
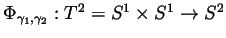 be defined by
for
be defined by
for
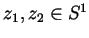 . Prove that the degree
. Prove that the degree
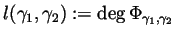 is invariant under
homotopies of
is invariant under
homotopies of 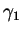 and
and 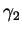 throughout which
throughout which 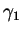 and
and
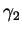 remain disjoint. (I.e., homotopies
remain disjoint. (I.e., homotopies
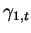 and
and
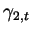 for which
for which
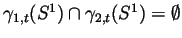 for all
for all 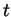 ).
).
- Compute (without worrying about signs, but otherwise with
justification) the degree
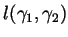 where
where 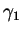 and
and
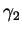 are given by the picture
are given by the picture
 .
.
- Compute (without worrying about signs, but otherwise with
justification) the degree
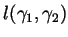 where
where 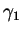 and
and
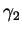 are given by the picture
are given by the picture  .
.
Problem 8.
- State the theorem about the homology of the complement of an embedded
disk in
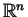 .
.
- State the theorem about the homology of the complement of an embedded
sphere in
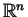 .
.
- Prove that the first of these two theorems implies the second.
Problem 9. A chain complex 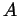 is said to be
``acyclic'' if its homology vanishes (i.e., if it is an exact sequence).
Let
is said to be
``acyclic'' if its homology vanishes (i.e., if it is an exact sequence).
Let 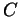 be a subcomplex of some chain complex
be a subcomplex of some chain complex 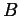 .
.
- Show that if
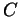 is acyclic then the homology of
is acyclic then the homology of 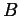 is isomorphic to
the homology of
is isomorphic to
the homology of 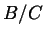 (so
(so 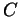 ``doesn't matter'').
``doesn't matter'').
- Show that if
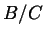 is acyclic then the homology of
is acyclic then the homology of 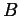 is isomorphic
to the homology of
is isomorphic
to the homology of 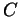 (so ``the part of
(so ``the part of 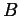 out of
out of 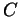 '' doesn't matter).
'' doesn't matter).
- If
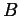 is acyclic, can you say anything about the relation between
the homology of
is acyclic, can you say anything about the relation between
the homology of 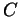 and the homology of
and the homology of 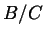 ?
?
Good Luck!
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2005-05-02
![]() be a topological space.
be a topological space.
![]() be a metric space.
be a metric space.
![]() be an
be an ![]() -dimensional
topological manifold (a space in which every point has a neighborhood
homeomorphic to
-dimensional
topological manifold (a space in which every point has a neighborhood
homeomorphic to
![]() ), and let
), and let ![]() be a point in
be a point in ![]() .
.
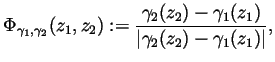
![]() is said to be
``acyclic'' if its homology vanishes (i.e., if it is an exact sequence).
Let
is said to be
``acyclic'' if its homology vanishes (i.e., if it is an exact sequence).
Let ![]() be a subcomplex of some chain complex
be a subcomplex of some chain complex ![]() .
.