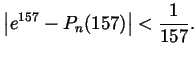Term Exam 4
University of Toronto, March 21, 2005
Solve all of the following 4 problems. Each problem is
worth 25 points. You have an hour and 50 minutes. Write your answers in
the Term Exam notebooks provided and not on this page.
Allowed Material: Any calculating device that is not
capable of displaying text.
Problem 1. Agents of
CSIS have secretly developed a
function 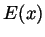 that has the following properties:
that has the following properties:
-
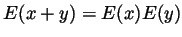 for all
for all
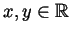 .
.
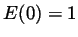
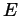 is differentiable at 0 and
is differentiable at 0 and 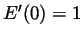 .
.
Prove the following:
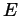 is everywhere differentiable and
is everywhere differentiable and 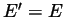 .
.
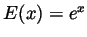 for all
for all
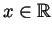 . The only lemma you may assume is that
if a function
. The only lemma you may assume is that
if a function 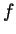 satisfies
satisfies 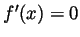 for all
for all 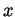 then
then 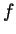 is a constant
function.
is a constant
function.
Problem 2. Compute the following integrals: (a few lines of
justification are expected in each case, not just the end result.)
-
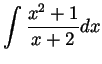 .
.
-
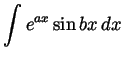 (assume that
(assume that
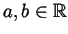 and that
and that
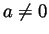 and
and 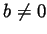 ).
).
-
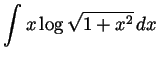 .
.
-
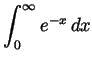 . (This, of course, is
. (This, of course, is
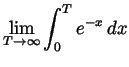 ).
).
Problem 3.
- State (without proof) the formula for the surface area of an object
defined by spinning the graph of a function
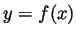 (for
(for
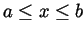 )
around the
)
around the 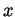 axis.
axis.
- Compute the surface area of a sphere of radius 1.
Problem 4.
- State and prove the remainder formula for Taylor polynomials (it is
sufficient to discuss just one form for the remainder, no need to mention
all the available forms).
- It is well known (and need not be reproven here) that the
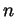 th
Taylor polynomial
th
Taylor polynomial
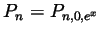 of
of 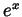 around 0 is given by
around 0 is given by
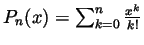 . It is also well known (and need not be
reproven here) that factorials grow faster than exponentials, so for any
fixed
. It is also well known (and need not be
reproven here) that factorials grow faster than exponentials, so for any
fixed 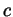 we have
we have
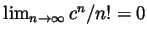 . Show that for large enough
. Show that for large enough 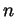 ,
,
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2005-03-23
![]() that has the following properties:
that has the following properties:
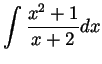 .
.
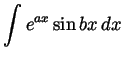 (assume that
(assume that
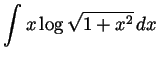 .
.
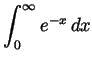 . (This, of course, is
. (This, of course, is
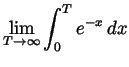 ).
).