The 13 Postulates
Everything you ever wanted to know about the real numbers is summarized
as follows. There is a set
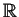 ``of real numbers'' with two binary
operations defined on it,
``of real numbers'' with two binary
operations defined on it, 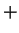 and
and 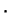 (``addition'' and
``multiplication''), two different distinct elements 0 and 1 and a
subset
(``addition'' and
``multiplication''), two different distinct elements 0 and 1 and a
subset
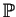 ``of positive numbers'' so that the following 13
postulates hold:
``of positive numbers'' so that the following 13
postulates hold:
- P1
- Addition is associative:
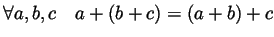 (``
(`` '' means ``for every'').
'' means ``for every'').
- P2
- The number 0 is an additive identity:
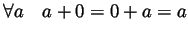 .
.
- P3
- Additive inverses exist:
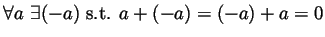 (``
(``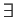 '' means ``there is'' or ``there exists'').
'' means ``there is'' or ``there exists'').
- P4
- Addition is commutative:
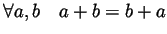 .
.
- P5
- Multiplication is associative:
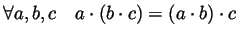 .
.
- P6
- The number 1 is a multiplicative identity:
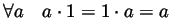 .
.
- P7
- Multiplicative inverses exist:
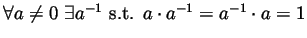 .
.
- P8
- Multiplication is commutative:
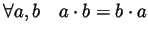 .
.
- P9
- The distributive law:
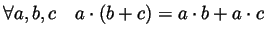 .
.
- P10
- The trichotomy for
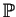 : for every
: for every 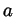 , exactly one of the
following holds:
, exactly one of the
following holds: 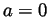 ,
,
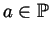 or
or
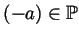 .
.
- P11
- Closure under addition: if
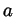 and
and 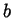 are in
are in 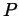 , then so is
, then so is
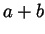 .
.
- P12
- Closure under multiplication: if
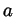 and
and 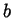 are in
are in 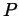 , then so is
, then so is
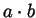 .
.
- P13
- The thirteenth postulate is the most subtle and interesting
of all. It will await a few weeks.
Here are a few corollaries and extra points:
- Sums such as
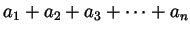 are well defined.
are well defined.
- The additive identity is unique. (Also multiplicative).
- Additive inverses are unique. (Also multiplicative).
- Subtraction can be defined.
-
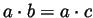 iff (if and only if)
iff (if and only if) 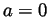 or
or 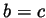 .
.
-
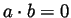 iff
iff 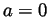 or
or 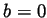 .
.
-
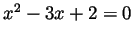 iff
iff 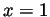 or
or 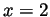 .
.
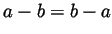 iff
iff 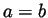 .
.
- A ``well behaved'' order relation can be defined (i.e., the booloean
operations
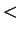 ,
, 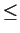 ,
, 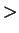 and
and 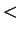 can be defined and they have some
expected properties).
can be defined and they have some
expected properties).
- The ``absolute value'' function
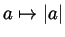 can be defined and for
all numbers
can be defined and for
all numbers 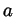 and
and 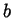 we have
we have
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2003-08-14
![]() ``of real numbers'' with two binary
operations defined on it,
``of real numbers'' with two binary
operations defined on it, ![]() and
and ![]() (``addition'' and
``multiplication''), two different distinct elements 0 and 1 and a
subset
(``addition'' and
``multiplication''), two different distinct elements 0 and 1 and a
subset
![]() ``of positive numbers'' so that the following 13
postulates hold:
``of positive numbers'' so that the following 13
postulates hold: