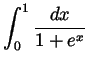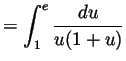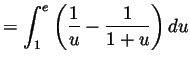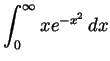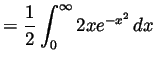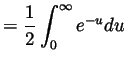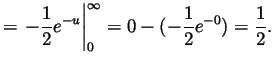Solution of Term Exam 3
Problem 1. Suppose that 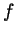 is nondecreasing on
is nondecreasing on ![$ [a,b]$](Solutionimg2.gif) .
Notice that
.
Notice that 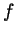 is automatically bounded on
is automatically bounded on ![$ [a,b]$](Solutionimg2.gif) , because
, because
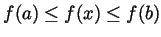 for any
for any 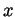 in
in ![$ [a,b]$](Solutionimg2.gif) .
.
- If
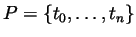 is a partition of
is a partition of ![$ [a,b]$](Solutionimg2.gif) , write formulas
for
, write formulas
for 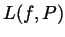 and
and 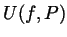 in as simple terms as possible.
in as simple terms as possible.
- Suppose that
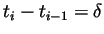 for each
for each 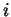 . Show that
. Show that
![$ U(f,P)-L(f,P)=\delta[f(b)-f(a)]$](Solutionimg10.gif) .
.
- Prove that
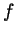 is integrable.
is integrable.
Solution. Notice that as 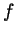 is nondecreasing,
is nondecreasing,
![$ m_i:=\inf_{[t_{i-1},t_i]}f(x)=f(t_{i-1})$](Solutionimg11.gif) and
and
![$ M_i:=\inf_{[t_{i-1},t_i]}f(x)=f(t_i)$](Solutionimg12.gif) . Hence,
. Hence,
- The upper and lower sums are given by
- If
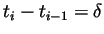 then
then
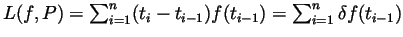 and likewise
and likewise
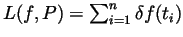 . Hence
. Hence
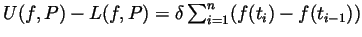 . By telescopic
summation, the last sum is
. By telescopic
summation, the last sum is
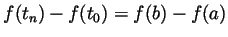 .
.
- Setting
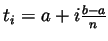 we get partitions with
we get partitions with
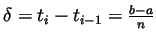 . This can be made arbitrariry
small, and hence
. This can be made arbitrariry
small, and hence
![$ U(f,P)-L(f,P)=\frac{b-a}{n}[f(b)-f(a)]$](Solutionimg21.gif) can be made
arbitrarily small, hence
can be made
arbitrarily small, hence 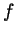 is integrable.
is integrable.
Problem 2. In each of the following, 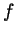 is a
continuous function on
is a
continuous function on ![$ [0,1]$](Solutionimg22.gif) .
.
- Show that
- Characterize the functions
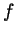 that have the property that
that have the property that
Solution.
- If
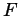 is a primitive of
is a primitive of 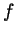 , i.e.,
, i.e., 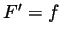 , then
, then
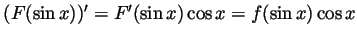 . Hence using the
second fundamental theorem of calculus,
. Hence using the
second fundamental theorem of calculus,
- Differentiate both sides of the equality
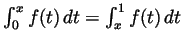 using the first fundamental theorem
of calculus and get that
using the first fundamental theorem
of calculus and get that
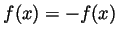 and thus that
and thus that 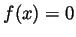 for all
for all 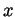 .
.
Problem 3.
- Prove that if two functions
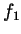 and
and 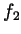 both satisfy
the differential equation
both satisfy
the differential equation 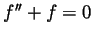 and if they have the same value
and the same first derivative at 0, then they are equal.
and if they have the same value
and the same first derivative at 0, then they are equal.
- Use the above to show that
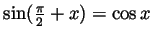 for all
for all
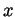 . (Do not use the formula for the
. (Do not use the formula for the 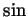 of a sum!)
of a sum!)
Solution.
- Set
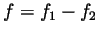 . As
. As
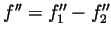 , it follows that
, it follows that 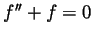 and clearly
and clearly
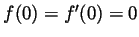 . Now set
. Now set
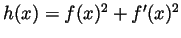 and
calculate
and
calculate
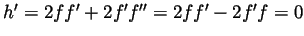 . Hence
. Hence 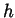 is a constant. But
is a constant. But
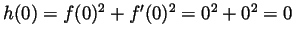 hence
hence 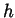 is the constant 0. But as
the two terms composing
is the constant 0. But as
the two terms composing 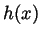 a non-negative, this forces each of
them to be 0, and in particular
a non-negative, this forces each of
them to be 0, and in particular 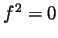 and thus
and thus
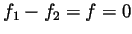 .
.
- Set
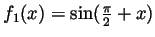 and
and
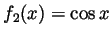 . Then
. Then
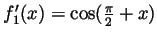 ,
,
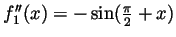 ,
,
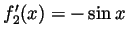 and
and
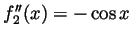 . Hence
. Hence 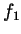 and
and 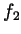 both
satisfy the differential equation
both
satisfy the differential equation 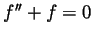 . In addition,
. In addition,
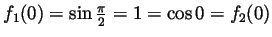 and
and
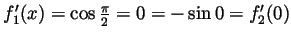 . Hence the requirements for
the theorem of the previous part of this problem are met, and hence its
conslusion is satisfied. So
. Hence the requirements for
the theorem of the previous part of this problem are met, and hence its
conslusion is satisfied. So 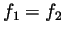 or
or
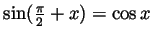 .
.
Problem 4.
- Compute
- Use your result to estimate the difference between
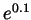 and
and
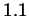 . Warning: a 10 digit answer obtained with your calculator may
contribute negatively to your grade. You shouldn't use any
calculating device and your derivation of the answer should be simple
enough that it be clear that you didn't need any machine help.
. Warning: a 10 digit answer obtained with your calculator may
contribute negatively to your grade. You shouldn't use any
calculating device and your derivation of the answer should be simple
enough that it be clear that you didn't need any machine help.
Solution.
- Using L'Hôpital's rule twice, we get
- From the above we get that
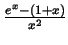 is
approximately
is
approximately 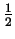 if
if 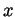 is small. Hoping that
is small. Hoping that 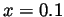 is small
enough, we find that
is small
enough, we find that
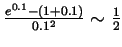 , meaning
that
, meaning
that
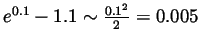 .
.
Problem 5. Evaluate the following integrals in terms of
elementary functions:
-
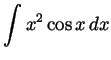
-
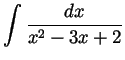 (cancelled)
(cancelled)
-
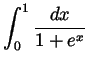
-
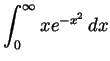
Solution.
- We integrate by parts twice:
- Not required, though still,
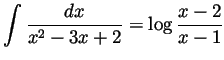 .
.
- Take
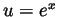 and then
and then
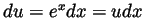 and hence
and hence
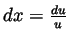 and
so
and
so
- Take
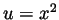 and then
and then 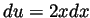 and so
and so
The results. 83 students took the exam; the average grade
is 65.31, the median is 65 and the standard deviation is 25.17.
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2003-02-17
![]() is nondecreasing on
is nondecreasing on ![]() .
Notice that
.
Notice that ![]() is automatically bounded on
is automatically bounded on ![]() , because
, because
![]() for any
for any ![]() in
in ![]() .
.
![]() is nondecreasing,
is nondecreasing,
![]() and
and
![]() . Hence,
. Hence,
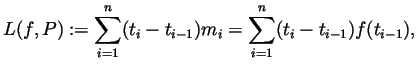
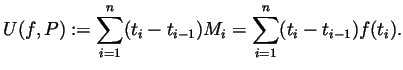
![]() is a
continuous function on
is a
continuous function on ![]() .
.
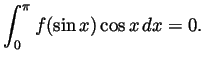
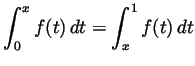 for all
for all 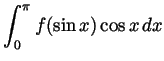
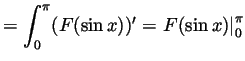
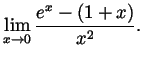
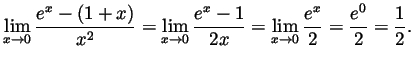
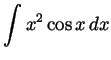
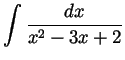 (cancelled)
(cancelled)
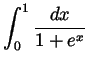
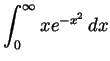
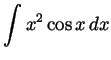
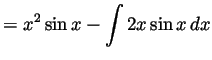
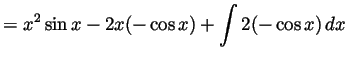
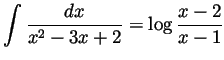 .
.