| Dror Bar-Natan: Classes: 2002-03: Math 157 - Analysis I: | (67) |
Next: Term Exam 1
Previous: Class Notes for the Week of October 14 (7 of 7) |
Solve the following 5 problems. Each is worth 20 points although they may have unequal difficulty. Write your answers in the space below the problems and on the front sides of the extra pages; use the back of the pages for scratch paper. Only work appearing on the front side of pages will be graded. Write your name and student number on each page. If you need more paper please ask the tutors. You have an hour and 50 minutes.
Allowed Material: Any calculating device that is not capable of displaying text.
(In the real exam each of the questions will appear on a separate page and there will be several blank pages stapled with your exam booklet. You will have space for your name and student number at the top of each page.)
Problem 1.
Problem 2. We say that a function ![]() is an inverse of a
function
is an inverse of a
function ![]() if
if
![]() , where
, where ![]() is the identity
function, defined by
is the identity
function, defined by ![]() for all
for all ![]() . Show that a function
. Show that a function ![]() has an
inverse
has an
inverse ![]() if and only if the following two conditions are satisfied:
if and only if the following two conditions are satisfied:
Problem 3. Sketch, to the best of your understanding, the graph of the function
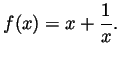
Problem 4. Suppose that ![]() is, for each natural number
is, for each natural number
![]() , some finite set of numbers and that
, some finite set of numbers and that ![]() and
and ![]() have no
members in common if
have no
members in common if ![]() . Define
. Define ![]() as follows:
as follows:
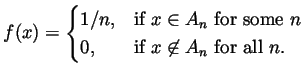
Problem 5. Suppose that ![]() satisfies
satisfies
![]() for all
for all ![]() and
and ![]() and that
and that ![]() is continuous at 0. Prove that
is continuous at 0. Prove that ![]() is
continuous everywhere.
is
continuous everywhere.
The generation of this document was assisted by LATEX2HTML.