$\newcommand{\const}{\mathrm{const}}$
Traffic flow is described by equation \begin{equation} \frac{\partial \rho}{\partial t}+ \frac{\partial q}{\partial x}=0 \label{equ-D.1} \end{equation} or \begin{equation} \frac{\partial \rho}{\partial t}+ \frac{\partial q}{\partial x}=f(x,t) \label{equ-D.2} \end{equation} where $\rho=\rho(x,t)$ is a density of cars on highway (i.e. numbers of cars at the segment of the length $dx$ is $\rho \,dx$, $q=q(x,t)$ is a flow of cars (i.e. number of cars crossing point $x$ from the left to the right for time $dt$ is $q\,dt$), and $f=f(x,t)$ is defined as $f=f_{in}-f_{out}$, $f_{in}\,dx dt$ and $f_{out}\,dx dt$ are numbers of cars entering/exiting highway for time $dt$ at the segment of the length $dx$) has been derived we need to connect $\rho$ and $q$.
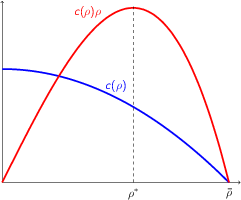
The simplest is $q=c \rho$ with a constant $c$: all cars are moving with the same speed $c$. Then (\ref{equ-D.1}) becomes \begin{equation} \frac{\partial \rho}{\partial t}+ c \frac{\partial \rho}{\partial x}=0. \label{equ-D.3} \end{equation} However more realistic would be $c=c(\rho)$ being monotone decreasing function of $\rho$ with $c(0)=c_0$ (speed on empty highway) and $c(\bar{\rho})=0$ where $\bar{\rho}$ is a density where movement is impossible. Assume that $q(\rho) = c(\rho)\rho$ has a single maximum at $\rho^*$. Then \begin{equation} \frac{\partial \rho}{\partial t}+ v \frac{\partial \rho}{\partial x}=0. \label{equ-D.4} \end{equation} with \begin{equation} v=v(\rho)= q'(\rho) = c(\rho)+ c' (\rho)\rho \label{equ-D.5} \end{equation} where $'$ is a derivative with respect to $\rho$. Therefore $\rho$ remains constant along integral line $x - v(\rho) t=\const$.
$v=v(\rho)$ is the group speed namely the speed with which point where density equals given density $\rho$ is moving. Here $v(\rho)< c(\rho)$ (because $c'<0$), so group speed is less than the speed of the cars (simply cars may join the group from behind and leave it from its front). Further $v>0$ as $\rho<\rho^*$ and $v<0$ as $\rho>\rho^*$; in the latter case the group moves backward: the jam grows faster than moves.
Also the integral lines may intersect (loose and faster moving group catches up with dense and slower group). When it happens $\rho$ becomes discontinuous, (\ref{equ-D.1}) still holds but (\ref{equ-D.4}) fails (it is no more equivalent to (\ref{equ-D.1}) ) and the theory becomes really complicated.
