$\newcommand{\erf}{\operatorname{erf}}$ $\newcommand{\const}{\mathrm{const}}$
In the previous lecture we considered heat equation \begin{equation} u_t=ku_{xx} \label{equ-11.1} \end{equation} with $x\in \mathbb{R}$ and $t>0$ and derived formula \begin{equation} u(x,t)=\int _{-\infty}^\infty G(x,x',t) g(x')\,dx'. \label{equ-11.2} \end{equation} with \begin{equation} G(x,x',t)=G_0(x-y,t):=\frac{1}{2\sqrt{k\pi t}}e^{-\frac{(x-x')^2}{4kt}} \label{equ-11.3} \end{equation} for solution of IVP $u|_{t=0}=g(x)$.
Similar formula was derived for heat equation on half-line or segment with the Dirichlet on Neumann boundary conditions.
Recall that $G(x,y,t)$ quickly decays as $|x-y|\to \infty$ and it tends to $0$ as $t\to +0$ for $x\ne y$, but $\int G(x,y,t)\,dy\to 1$ as $t\to +0$.
Now we claim that for 2D and 3D heat equations \begin{align} &u_t=k\bigl(u_{xx}+u_{yy}\bigr), \label{equ-11.4}\\ &u_t=k\bigl(u_{xx}+u_{yy}+u_{zz}\bigr), \label{equ-11.5} \end{align} similar formulae hold: \begin{align} &u=\iint G_2 (x,y;x',y';t) g(x',y')\,dx'dy', \label{equ-11.6}\\ &u=\iiint G_3 (x,y,z;x',y',z';t) g(x',y',z')\,dx'dy'dz' \label{equ-11.7} \end{align} with \begin{align} &G_2 (x,y;x',y';t) =&& G_1(x,x',t)G_1(y,y',t), \label{equ-11.8}\\ &G_3 (x,y,z;x',y',z';t) =&& G_1(x,x',t)G_1(y,y',t)G_1(z,z',t); \label{equ-11.9} \end{align} in particular for the whole $\mathbb{R}^n$ \begin{align} &G_n (\mathbf{x},\mathbf{x}';t) =&& (2\sqrt{\pi k t})^{-n/2}e^{-\frac{|\mathbf{x}-\mathbf{x}'|}{4kt}}. \label{equ-11.10} \end{align}
To justify our claim we note that
$G_n$ satisfies $n$-dimensional heat equation. Really, consider f.e. $G_2$: \begin{align*} G_{2\,t} (x,y;x',y';t) =& G_{1\,t}(x,x',t)G_1(y,y',t)+G_1(x,x',t)G_{1.t}(y,y',t)=\\ & kG_{1\,xx}(x,x',t)G_1(y,y',t)+kG_1(x,x',t)G_{1\,yy}(y,y',t)=\\ &k \Delta \bigl( G_{1\,t}(x,x',t)G_1(y,y',t) \bigr)= k\Delta G_2(x,y;x',y';t) \end{align*}
$G_n (\mathbf{x},\mathbf{x}';t)$ quickly decays as $|\mathbf{x}-\mathbf{x}'|\to \infty$ and it tends to $0$ as $t\to +0$ for $\mathbf{x}\ne \mathbf{x}'$, but
$\int G(\mathbf{x},\mathbf{x}',t)\,dy\to 1$ as $t\to +0$;
$G(\mathbf{x},\mathbf{x}',t)=G(\mathbf{x}',\mathbf{x},t)$.
The last three properties are due to the similar properties of $G_1$.
Properties (a)-(d) imply integral representation (\ref{equ-11.6}) (or its $n$-dimensional variant).
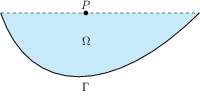
Consider heat eqution in the domain $\Omega$ like below

We claim that
Proposition 1 (maximum principle). Let $u$ satisfy heat equation in $\Omega$. Then \begin{equation} \max _\Omega u = \max _\Gamma u. \label{equ-11.11} \end{equation}
Almost correct proof. Let (\ref{equ-11.11}) be wrong. Then there exist point $P=(\bar{x},\bar{t})\in \Omega\setminus \Gamma$ s.t. $u$ reaches its maximum at $P$. Without any loss of the generality we can assume that $P$ belongs to an upper lid of $\Omega$. Then \begin{equation} u_t(P )\ge 0 \label{equ-11.12} \end{equation} (really $u(\bar{x},\bar{t})\ge u(\bar{x},t)$ for all $t: \bar{t}>t>\bar{t}-\epsilon$ and then $\bigl( u(\bar{x},\bar{t})-u(\bar{x},t)\bigr)/(\bar{t}-t)\ge 0$ and as $t\nearrow \bar{t}$) we get (\ref{equ-11.12}).
Also $u_{xx}( P)\le 0$ (really $u(x,\bar{t})$ reaches maximum as $x=\bar{x}$). This inequality combined with (\ref{equ-11.12}) almost contradict to heat equation (almost because there could be equalities).
Correct proof. Note first that the above arguments prove (\ref{equ-11.11}) if $u$ satisfies inequality $u_t-ku_{xx}<0$ because then there will be contradiction.
Note that $v= u-\varepsilon t$ satisfies $v_t-kv_{xx}<0$ for any $\varepsilon >0$ and therefore \begin{equation*} \max _\Omega (u-\varepsilon t) = \max _\Gamma (u-\varepsilon t). \end{equation*} Taking limit as $\varepsilon \to +0$ we get (\ref{equ-11.11}).
Remark.
Sure, the same proof works for multidimensional heat equation.
In fact, either in $\Omega \setminus \Gamma$ $u$ is strictly less than $\max _\Gamma u$ or $u=\const$. The proof is a bit more sophisticated.
Corollary 1 (minimum principle). \begin{equation} \min _\Omega u = \min _\Gamma u. \label{equ-11.13} \end{equation} Really, $-u$ also satisfies heat equation.
Corollary 2. $u=0$ everywhere on $\Gamma$ $\implies u=0$ everywhere on $\Omega$.
Really, then $\max _\Omega u=\min_\Omega u=0$.
Corollary 3. Let $u,v$ both satisfy heat equation. Then $u=v$ everywhere on $\Gamma$ $\implies u=v$ everywhere on $\Omega$.
Really, then $(u-v)$ satisfies heat equation.
See Problem 6 of Home Assignment 3.