$\newcommand{\const}{\mathrm{const}}$
We solved IVP with homogeneous ($=0$) initial data for inhomogeneous wave equation. Now consider both inhomogeneous data and equation. So we consider problem (4.6)-(4.8): \begin{align} &u_{tt}-c^2u_{xx}=f(x,t),\label{eq-1} \\[3pt] &u|_{t=0}=g(x),\label{eq-2}\\[3pt] &u_t|_{t=0}=h(x). \label{eq-3} \end{align} when neither $f$, nor $g,h$ are necessarily equal to $0$.
The good news is that our equation is linear and therefore $u=u_2+u_1$ where $u_1$ satisfies problem with right-hand function $f(x,t)$ but with $g$ and $h$ replaced by $0$ and $u_2$ satisfies the same problem albeit with $f$ replaced by $0$ and original $g,h$: \begin{align*} &u_{1tt}-c^2u_{1xx}=f(x,t), \qquad &&u_{2tt}-c^2u_{2xx}=0, \\[3pt] &u_1|_{t=0}=0, && u_2|_{t=0}=g(x),\\[3pt] &u_{1t}|_{t=0}=0 &&u_{2t}|_{t=0}=h(x). \end{align*}
Exercise. Prove it.
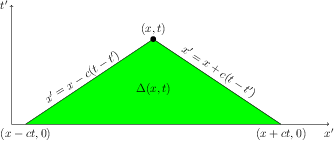
Then $u_1$ is given by (4.11), and $u_2$ is given by (3.14) (with $(f,g)\mapsto (g,h)$)and adding them we arrive to the final \begin{multline} u(x,t)= \underbracket{\frac{1}{2}\bigl[ g(x+ct)+g(x-ct)\bigr]+\frac{1}{2c}\int_{x-ct}^{x+ct} h(y)\,dy}_{=u_2}+\\[3pt] \underbracket{\frac{1}{2c} \iint_{\Delta (x,t)} f(x',t' )\,dx\,d t' }_{=u_1}. \label{eq-4} \end{multline} where recall that $\Delta(x,t)$ is a characteristic triangle:

This formula is also called D'Alembert formula.
Remark. Note that integral of $h$ in $u_2$ is taken over base of the characteristic triangle $\Delta(x,t)$ and $g$ is taken in the ens of this base.
We discuss formula (\ref{eq-4}) in details in the next lecture and now let us derive it by a completely different method. Again, in virtue of (3.14) we need to consider only the case when $g=h=0$.
Let us define an auxillary function $U(x,t,\tau)$ ($0<\tau<t$) as a solution of an auxillary problem \begin{align} &U_{tt}-c^2U_{xx}=0,\label{eq-5} \\[3pt] &U|_{t=\tau}=0,\label{eq-6}\\[3pt] &U_t|_{t=\tau}=f(x,\tau). \label{eq-7} \end{align} We claim that
Proposition. \begin{equation} u(x,t)=\int_0^t U(x,t,\tau)\,d\tau \label{eq-8} \end{equation} is a required solution.
Proof. Note first that we can differentiate (\ref{eq-8}) by $x$ easily: \begin{equation} u_x=\int_0^t U_x (x,t,\tau)\,d\tau,\qquad u_{xx}=\int_0^t U_{xx} (x,t,\tau)\,d\tau \label{eq-9} \end{equation} and so on. Let us find $u_t$. Note that $u$ depends on $t$ through its upper limit and through integrand. We apply formula \begin{multline} \frac{d\ }{dt}\Bigl(\int_{\alpha(t)}^{\beta(t)} F (t,\tau)\,d\tau\Bigr) =\\ -F(t,\alpha(t))\alpha'(t)+F(t,\beta(t))\beta'(t)+ \int_{\alpha(t)}^{\beta(t)} \frac{\partial F}{\partial t} (t,\tau)\,d\tau\qquad \label{eq-10} \end{multline} which you should know but we will prove it anyway.
As $\alpha=0$, $\beta=t$ we have $\alpha'=0$, $\beta'=1$ and \begin{equation*} u_t=U(x,t,t)+\int_0^t U_t (x,t,\tau)\,d\tau. \end{equation*} But $U(x,t,t)=0$ due to (\ref{eq-6})) and therefore \begin{equation} u_t=\int_0^t U_t (x,t,\tau)\,d\tau. \label{eq-11} \end{equation} We can differentiate this with respect to $x$ as in (\ref{eq-9}). Let us differentiate by $t$. Applying the same (\ref{eq-10}) we get \begin{equation*} u_{tt}=U_t(x,t,t)+\int_0^t U_{tt} (x,t,\tau)\,d\tau. \end{equation*} Due to (\ref{eq-7}) $U_t(x,t,t)=f(x,t)$: \begin{equation*} u_{tt}=f(x,t)+\int_0^t U_{tt} (x,t,\tau)\,d\tau. \end{equation*} Therefore \begin{equation*} u_{tt}-c^2u_{xx}=f(x,t)+\int_0^t \underbracket{\bigl(U_{tt}-c^2U_{xx}\bigr)}_{=0} (x,t,\tau)\,d\tau =f(x,t) \end{equation*} where integrand vanishes due to (\ref{eq-5}). So, $u$ really satisfies (\ref{eq-1}). Due to (\ref{eq-8}) and (\ref{eq-11}) $u|_{t=0}=u_t|_{t=0}=0$. QED.
Formula (\ref{eq-8}) is Duhamel integral formula.
Remark. It is not important that it is wave equation: we need assume that equation is linear and has a form $u\_{tt} + Lu=f$ where $Lu$ is a linear combination of $u$ and its derivatives but with no more than $1$ differentiation by $t$.
Now we claim that \begin{equation} U(x,t,\tau)= \frac{1}{2c} \int _{x-c(t-\tau)} ^{x+c(t-\tau)} f(x',\tau)\,dx'. \label{eq-12} \end{equation} Really, changing variable $t'=t-\tau$ we get the same problem albeit with $t'$ instead of $t$ and with initial data at $t'=0$.
Plugging (\ref{eq-12}) into (\ref{eq-8}) we get \begin{equation} u(x,t)=\int_0^t \frac{1}{2c} \Bigl[\int_{x-c(t-\tau)} ^{x+c(t-\tau)} f(x',\tau)\,dx'\Bigr]\,d\tau. \label{eq-13} \end{equation}
Exercise. Rewrite double integral (\ref{eq-13}) as a $2D$-integral in the right-hand expression of (4.11).
Proof of (\ref{eq-10}). Let us plug $\gamma$ into $F(x,t,\tau)$ instead of $t$. Then integral $I(t)=J(\alpha(t),\beta(t),\gamma(t))$ with $J(\alpha,\beta,\gamma)=\int_\alpha^\beta F(\gamma,\tau)\,d\tau$ and by chain rule $I'(t)=J_\alpha \alpha'+J_\beta \beta'+J_\gamma \gamma'$.
But $J_\alpha=-F(\gamma,\alpha)$, $J_\beta=F(\gamma,\beta)$ (differentiation by lower and upper limit) and $J_\gamma=\int_\alpha^\beta F_\gamma (\gamma,\tau)\,d\tau$. Plugging $\gamma=t$, $\gamma'=1$ we arrive to (\ref{eq-10}).