![\[
\sqrt[n]{a_1a_2\ldots a_n}\leq\frac{a_1+a_2+\cdots+a_n}{n}
\]](index_1.gif)
There is a little known lovely geometric counterpart to the well known Arithmetic/Geometric Means Inequality. The inequality says that for every sequence of positive numbers a1, a2, ..., an, the geometric mean of these numbers is smaller than or equal to the arithmetic mean of these numbers:
![\[
\sqrt[n]{a_1a_2\ldots a_n}\leq\frac{a_1+a_2+\cdots+a_n}{n}
\]](index_1.gif)
If we multiply both sides of this inequality by n and raise to the nth power, we come to:
![\[
n^n\cdot a_1a_2\ldots a_n\leq(a_1+a_2+\cdots+a_n)^n
\]](index_2.gif)
This leads to a very natural question:
Question. Is it possible to pack nn rectangular n-dimensional boxes whose sides are a1, a2, ..., an inside one big n-dimensional cube whose side is a1+a2+...+an?
This question is much harder than it seems! It implies the inequality of the means, of course, but it is not implied by it. Here's almost all that is known:
The case of n=2: Here one needs to place 4 rectangles of size a by b inside one square whose side is a+b. Even this is not entirely trivial, though it is not too hard. You find the solution as the background image to this page and even sometimes as bathroom tiles!
The case of n=3: Now this is a much harder problem. It is quite impossible to solve it without a physical model, and you'll only appreciate how hard it is if you get a physical model and spend a few hours with it. Here's one made of wood, along with a failed attempt to assemble it (the last wall of boxes wouldn't fit and there's too much useless leftover space at the top):

You can also make a paper/cardboard model. Just click on the two images below to download two PDF files. Print the first once and the second seven times, cut along the full lines, fold along the dashed lines, and glue as marked. Thicker paper is better!
 the big cube |
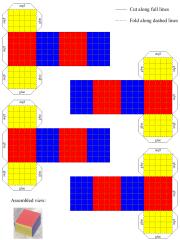 the boxes |
Let me say that again - fitting these 27 boxes inside this one cube is a hard exercise! If you despair, check out the solution sequence below. It's actually harmless to see the solution even if you intend to work on the puzzle later on - the solution is quite unmemorable, and unless you make a conscious effort to memorize it, you're going to forget it right away. You can also click on the Mosaic or Layers buttons below and get a printable key to the solution.

The case of n=4: Somewhat surprisingly, the case of n=4 is easier than the case of n=3, for there is a solution in this case which has a simple algebraic origin and a simple combinatorial description. We only give a hint:
Hint. Use the case of n=2 three times to translate the following algebraic argument to a specific way to assemble 256 boxes of sides a by b by c by d inside a single cube of side a+b+c+d:
![\[
\sqrt[4]{abcd} = \sqrt{\sqrt{ab}\sqrt{cd}}
\leq \sqrt{\frac{a+b}{2}\cdot\frac{c+d}{2}}
\leq \frac{\frac{a+b}{2} + \frac{c+d}{2}}{2}
= \frac{a+b+c+d}{4}.
\]](index_3.gif)
The case of n=5 is wide open. If you can do it and all higher unknown cases, you'll be famous! After all, we are in the 21st century and its not so easy to come up with new proofs of high-school level inequalities.
Did you try to program it? For n=5, one has to place 55=3,125 boxes, and each one has 5!=120 possible orientations. Thus there are 1203,125 possibilities to start with, and we don't know how many of them are good (i.e., have no internal clashes and do not extrude out of the cube. So an exhaustive search is out of question. (In fact, merely testing if a given proposed solution is indeed a solution is a non-trivial proposition. There are 171,584 pairs of diagonally neighboring boxes so 171,584 potential internal clashes, and another 3,125 ways a box may extrude out of the cube.)
I did try to program it nevertheless. We don't know how many solutions there are for n=5. Possibly none, possibly few, possibly very very many. In the last case, we have a chance of finding one. So I wrote a program that starts from some arbitrary proposed solution, and then uses simulated annealing to try and lower the number of "problems" it has. Here's a short summary of the results:
While a failure, my programing attempt does raise some interesting mathematical questions. Some future edition of this document may contain a summary of those.
The cases of n>5: These are divided in two: the simple and the hopeless. An argument similar to that of the case of n=4 shows that if we know a solution in dimension m and a solution in dimension n, then we can "compose" them and get a solution in dimension mn. Given that we know solutions in dimensions 2 and 3, it follows that we can find solutions in dimension 2p3q for all p and q. Everything else seems hopeless.
Reference. Everything in this page (except the pictures and the program) comes from Berlekamp, Conway and Guy's Winning Ways for Your Mathematical Plays, Academic Press, New York 1983.
Displayed equations by HTMX.
Some artwork and painting by Amir, Assaf and Itai.
Thanks to Kumar Murty and Ehud
de Shalit for pointing out a typo in an earlier version of this
page.