Finite Type Invariants by the Species
Dror Bar-Natan
Date:
This Edition: Mar. 19, 2000;
First Edition: This is merely an unifinished draft;
Revision History: Section 6.
Institute of Mathematics
The Hebrew University
Giv'at-Ram, Jerusalem 91904
Israel
drorbn@math.huji.ac.il
Abstract:
We study the general theory of finite type invariants through the study
of examples.
Alternative
formats |
 |
 |
 |
 |
| Sizes |
106Kb |
299Kb |
379Kb |
486Kb |
The  version exists in a SPLIT edition
(about 27 html files and 152 images) for
easier browsing, in a LONG edition
(one html file, about 152 images) for easier searching
and printing, and in a TAR.GZ version
(194Kb) for offline browsing.
version exists in a SPLIT edition
(about 27 html files and 152 images) for
easier browsing, in a LONG edition
(one html file, about 152 images) for easier searching
and printing, and in a TAR.GZ version
(194Kb) for offline browsing.
1. Introduction
In the late 1980s, Vassiliev [Va1,Va2]
suggested to study knot invariants by studying the space of all
knots. The first new ingredient thus added is the notion of
``neighboring'' knots, knots that differ in only one crossing, and
the idea that one should study how knot invariants change in the
``neighborhood'' of a given knot. This idea led to a definition
of a certain class of knot invariants, now known as ``Vassiliev''
or ``finite type'' invariants. By now more than 350 papers have been
written on the subject; see [B-N2]. Vassiliev's original
definition (independently discovered by Goussarov [Go1,Go2] at roughly the same time) was formalized
in a different way by Birman and Lin [BL],
and later re-interpreted by analogy with multi-variable calculus by
Bar-Natan [B-N1].
The basic idea in Bar-Natan [B-N1] was that
differences are ``cousins'' of derivatives, and hence one should
think of the difference between the values of a knot invariant
V on two neighboring knots as a ``derivative'' of the original
invariant. Repeating this, we find that iterated differences (as
considered by [Va1,Va2,Go1,Go2,BL,B-N1])
of values of V in the neighborhood of some knot should be thought of
as multiple derivatives. A ``Vassiliev'' or ``finite type'' invariant
of type m is then the analog of a polynomial -- an invariant whose
m+1st derivatives, or m+1st iterated differences, vanishes.
Clearly, these ideas are very general, and knots (and even topology in
general) are just a particular case. Whenever an appropriate notion of
``neighborhood of an object'' exists, one can talk about finite type
invariants of such objects. This leads to many different ``species''
of finite type invariants. Let us mention just a few:
- The usual notion of nearness of knots, knots that differ at only
a single crossing, leads to the usual Vassiliev invariants.
- Similarly, one can define ``Vassiliev'' invariants of braids, links,
tangles, knotted graphs, etc.
- Goussarov [Go3] has also an alternative
notion of a neighborhood of a knot (or link), defined by
``interdependent modifications''. This notion leads to a different
(though at the end, equivalent) theory of finite type invariants of
knots and links.
- Two algebraically split links (links whose linking numbers all vanish)
can be considered neighboring if they differ by the simultaneous flip of
two opposite crossings between two given components (such a double
flip preserves linking numbers, whereas a single flip doesn't). See
Figure 1. This leads to a little known but probably
interesting theory of finite type invariants of algebraically split
links.
Figure 1:
A move that preserves linking numbers.
![\begin{figure}
\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in...
...draws/ASMove.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img7.gif) |
- Several authors [] have considered several notions of finite type
invariants of plane curves.
- Ohtsuki [Oh1] considers two integral
homology spheres to be neighboring (roughly) if they differ by a single
surgery. This leads to a notion of finite type invariants of integral
homology spheres. Several variants of his definition were considered
in [Ga1,GL1,GO1,GL2,GO2,Ga2,GL3]
A finite type theory automatically comes bundled with several spaces
that play a significant role in it. In the best known case of knots,
these are the spaces of chord diagrams, 4T relations, weight systems,
chord diagrams modulo 4T relations, relations between 4T relations,
and a few lesser known spaces that should probably be better known. There
is a ``general theory of finite type invariants'', defined in terms of
these spaces, in which one attempts to classify finite type invariants by
first classifying their potential mth derivatives, and then by studying
which of those potential derivatives can actually be integrated to an
honest invariant. I should say that though this ``general theory'' is
rather small, it is also rather interesting (with the most interesting
parts developed by M. Hutchings [Hu] and
private communication), and insufficiently well known even in the
case of the usual finite type invariants of knots.
The purpose of this paper is twofold:
- 1.
- To state (and propagate) this general theory of finite type
invariants of anything. Namely, to construct, name, and study
the relationships between those spaces that come automatically
with every finite type theory, especially from the perspective of
the integration theory of ``weight systems''. We first do it in
Section 1 on a well known example, the original finite
type theory of knots. We then extract some general features from this
example and give them general names; this is done in the rather short
Section 2.
- 2.
- To list many of the currently known finite type theories, and
figure out (to the degree that is now possible) what these associated
spaces are on a species by species basis. Our list takes the form of a
``classification''1.
The top subdivision is into the classes of ``Knotted Objects'',
``3-Manifolds'' and ``Plane Curves'', and these classes are
described in Sections 4, 5
and 6, respectively.
Acknowledgement: I wish to thank Mike Hutchings for the inspiration
to write this paper and for telling me his ideas about integration
theory. I also wish to thank E. Appleboim and H. Scolnicov for many
ideas and conversations.
1. The case of knots
As we have already indicated in the introduction, the finite type theory
for knots (Vassiliev theory) is built around the notions of n-singular
knots, and differences between overcrossings and undercrossings. Let us
make those notions precise:
Definition 1.1
An
n-singular knot is an oriented knot in an oriented
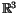
,
which is allowed to have
n singular points that locally look like
the image in Figure
2. For simplicity in the later
parts of this section, we only consider framed (singular or not) knots,
and always use blackboard framing when a knot projection or a part of
a knot projection is drawn.
Figure 2:
A singular point.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...s/DoublePoint.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img11.gif) |
Definition 1.2
Let
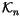
be the

-module freely generated by all
n-singular
knots, modulo the following ``co-differentiability relation'':
Notice that
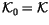
is simply the free

-module generated by
all (framed) knots.
Definition 1.3
Let

be defined by
``resolving'' any one of the singular points in an (
n+1)-singular knot in

:
![\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
\raisebox{8...
...pt}{ \input draws/deltadef.tex }
\hspace{-1.9mm}
\end{array}
\end{displaymath}](img18.gif) |
(1) |
Note that thanks to the co-differentiability relation,
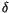
is well
defined. It is called ``the co-derivative''. We denote the adjoint of
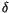
by
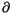
and call it ``the derivative''. It is a map
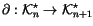
.
The name ``derivative'' is justified by the fact that
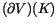 for some
for some
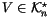 and
and
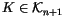 is by definition
the difference of the values of V on two ``neighboring'' n-singular
knots, in harmony with the usual definition of derivative for functions
on
is by definition
the difference of the values of V on two ``neighboring'' n-singular
knots, in harmony with the usual definition of derivative for functions
on
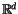 .
.
Definition 1.4
An invariant of knots
V (equivalently, a

-linear functional on
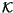
)
is said to be of finite type
n if
its (
n+1)-st derivative vanishes, that is, if
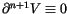
.
(This definition is the analog of one of the standard definitions of
polynomials on
).
When thinking about finite type invariants, it is convenient to have in
mind the following ladders of spaces and their duals, printed here with the
names of some specific elements that we will use later:
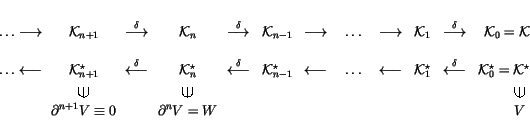 |
(2) |
One may take the definition of a general ``theory of finite type
invariants'' to be the data in (2), with arbitrary
``n-singular objects'' replacing the n-singular knots. Much
of what we will say below depends only on the existance of the
ladders (2), or on the existance of certain natural
extensions thereof, and is therefore quite general.
As promised in the introduction, we study invariants of type n by
studying their nth derivatives. Clearly, if V is of type n and
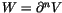 ,
then
,
then
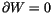 (``W is a constant''). Glancing
at (2), we see that W descends to a linear functional,
also called W, on
(``W is a constant''). Glancing
at (2), we see that W descends to a linear functional,
also called W, on
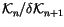 :
:
Definition 1.5
We call
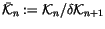
the space of ``
n-symbols'' associated with the ladders
in (
2). (The name is inspired by the theory of differential
operators, where the ``symbol'' of an operator is essentially its
equivalence class modulo lower order operators. The symbol is responsible
for many of the properties of the original operator, and for many
purposes, two operators that have the same symbol are ``the same''.)
We denote the projection mapping
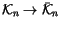
that maps every
singular knot to its symbol by
.
The following classical proposition (see e.g. [B-N1,Bi,BL,Go1,Go2,Ko1,Va1,Va2] identifies the space of n-symbols in our case:
Proposition 1.6
The space
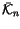
of
n-symbols for (
2) is
canonically isomorphic to the space
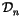
of
n-chord diagrams,
defined below.

Definition 1.7
An
n-chord diagram is a choice of
n pairs of
distinct points on an oriented circle, considered up to orientation
preserving homeomorphisms of the circle. Usually an
n-chord diagram is
simply drawn as a circle with
n chords (whose ends are the
n pairs),
as in the 5-chord example in Figure
3. The space
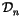
is the space of all formal

-linear combinations of
n-chord diagrams.
Figure 3:
A chord diagram.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...draws/5Chords.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img37.gif) |
Next, we wish to find conditions that a ``potential top derivative'' has
to satisfy in order to actually be a top derivative. More precisely, we
wish to find conditions that a functional
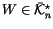 has
to satisfy in order to be
has
to satisfy in order to be
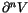 for some invariant V. A first
condition is that W must be ``integrable once''; namely, there has to
be some
for some invariant V. A first
condition is that W must be ``integrable once''; namely, there has to
be some
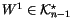 with
with
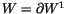 .
Another quick
glance at (2), and we see that W is integrable once iff
it vanishes on
.
Another quick
glance at (2), and we see that W is integrable once iff
it vanishes on
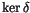 ,
which is the same as requiring that Wdescends to
,
which is the same as requiring that Wdescends to
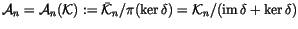 (there should be no confusion
regarding the identities of the
(there should be no confusion
regarding the identities of the 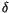 's involved). Often elements of
's involved). Often elements of
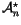 are refered to as ``weight systems''. A more accurate
name would be ``once-integrable weight systems''.
are refered to as ``weight systems''. A more accurate
name would be ``once-integrable weight systems''.
We see that it is necessary to understand
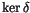 .
In
Figure 4 we show a family of members of
.
In
Figure 4 we show a family of members of
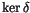 ,
the
``Topological 4-Term'' (T4T) relations. Figure 5 explains
how they arise from ``lassoing a singular point''. The following theorem
says that this is all:
,
the
``Topological 4-Term'' (T4T) relations. Figure 5 explains
how they arise from ``lassoing a singular point''. The following theorem
says that this is all:
Figure 4:
A Topological 4-Term (T4T) relation. Each of the four graphics in the
picture represents a part of an n-singular knot (so there are n-2 additional singular points not shown), and, as usual in knot theory, the
4 singular knots in the equation are the same outside the region shown.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...put draws/T4T.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img45.gif) |
Figure 5:
Lassoing a singular point: Each of the graphics represents an
(n-1)-singular knot, but only one of the singularities is explicitly
displayed. Start from the left-most graphic, pull the ``lasso'' under
the displayed singular point, ``lasso'' the singular point by crossing
each of the four arcs emenating from it one at a time, and pull the
lasso back out, returning to the initial position. Each time an arc is
crossed, the difference between ``before'' and ``after'' is the
co-derivative of an n-singular knot (up to signs). The four
n-singular knot thus obtained are the ones making the Topological
4-Term relation, and the co-derivative of their signed sum is the
difference between the first and the last (n-1)-singular knot shown
in this figure; namely, it is 0.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...t draws/Lasso.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img46.gif) |
Pushing the T4T relations down to the level of symbols, we get the
well-known 4T relations, which span
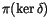 :
(see
e.g. [B-N1])
:
(see
e.g. [B-N1])
We thus find that
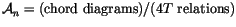 ,
as usual in the theory of finite type invariants of knots.
,
as usual in the theory of finite type invariants of knots.
We have so far found that if V is a type-n invariant, then
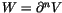 is a linear functional on
is a linear functional on
 .
A question arises
whether every linear functional on
.
A question arises
whether every linear functional on
 arises in this way. At least
if the ground ring is extended to
arises in this way. At least
if the ground ring is extended to
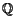 ,
the answer is positive:
,
the answer is positive:
Theorem 2 (The Fundamental Theorem of
Finite Type Invariants, Kontsevich [
Ko1])
Over
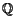
,
for every
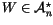
there exists a type
ninvariant
V with
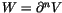
.
In other words, every once-integrable
weight system is fully integrable.
The problem with the Fundamental Theorem is that all the proofs we have
for it are somehow ``transcendental'', using notions from realms outside
the present one, and none of the known proofs settles the question over
the integers (see [BS]). In this section
we describe what appears to be the most natural and oldest approach to
the proof, having been mentioned already in [Va1,BL]. Presently, we are stuck and the so-called
``topological'' approach does not lead to a proof. But it seems to me that
it's worth studying further; when something natural fails, there ought to
be a natural reason for that, and it would be nice to know what it is.
The idea of the topological approach is simple: To get from W to
V, we need to ``integrate'' n times. Let's do this one integral at
a time. By the definition of
 ,
we know that we can integrate
once and find
,
we know that we can integrate
once and find
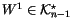 so that
so that
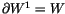 .
Can
we work a bit harder, and find a ``good'' W1, so that there would
be a
.
Can
we work a bit harder, and find a ``good'' W1, so that there would
be a
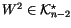 with
with
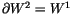 ? Proceeding like
that and assuming that all goes well along the way, we would end with a
? Proceeding like
that and assuming that all goes well along the way, we would end with a
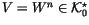 with
with
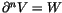 ,
as required. Thus we are
naturally lead to the following conjecture, which implies the Fundamental
Theorem by the backward-inductive argument just sketched:
,
as required. Thus we are
naturally lead to the following conjecture, which implies the Fundamental
Theorem by the backward-inductive argument just sketched:
Conjecture 1
Every once-integrable invariant of
n-singular knots also twice
integrable. Glancing at (
2), we see that this is the same
as saying that
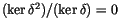
.
This conjecture is somewhat stronger than Theorem 2.
Indeed, Theorem 2 is equivalent to
Conjecture 1 restricted to the case when the given
invariant has some (possibly high) derivative identically equal to 0(exercise!). But it is hard to imagine a topological proof of the
restricted form of Conjecture 1 that would not prove
it in full.
The difficulty in Conjecture 1 is that it's hard
to say much about
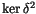 .
In [Hu],
Michael Hutchings was able to translate the statement
.
In [Hu],
Michael Hutchings was able to translate the statement
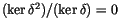 to an easier-looking
combinatorial-topological statement, which is implied by
and perhaps equivalent to an even simpler fully combinatorial
statement. Furthermore, Hutchings proved the fully combinatorial statement
in the analogous case of finite type braid invariants, thus proving
Conjecture 1 and Theorem 2
(over
to an easier-looking
combinatorial-topological statement, which is implied by
and perhaps equivalent to an even simpler fully combinatorial
statement. Furthermore, Hutchings proved the fully combinatorial statement
in the analogous case of finite type braid invariants, thus proving
Conjecture 1 and Theorem 2
(over
 )
in that case, and thus proving the viability of his
technique.
)
in that case, and thus proving the viability of his
technique.
Hutchings' first step was to write a chain of isomorphisms reducing
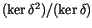 to something more manageable. Our next step
will be to introduce all the spaces participating in Hutchings' chain.
First, let us consider the space of all T4T relations:
to something more manageable. Our next step
will be to introduce all the spaces participating in Hutchings' chain.
First, let us consider the space of all T4T relations:
Definition 1.8
Let
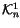
be the

-module generated by all (framed) knots
having
n-2 singularities as in Definition
1.1,
and plus one additional ``Topological Relator'' singularity
that locally looks like the image in Figure
6,
modulo the same co-differentiability relations as in
Definition
1.2. Define
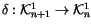
in the same way as for knots, using equation (
1). Finally,
define
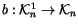
by mapping the topological relator to
the topological 4-term relation, the 4-term alternating sum inside the
paranthesis in Figure
4.
Figure 6:
The ``Topological Relator'' singularity.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...ogicalRelator.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img65.gif) |
The spaces
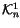 form a ladder similar to the one
in (2), and, in fact, they combine with the ladder
in (2) to a single commutative diagram:
form a ladder similar to the one
in (2), and, in fact, they combine with the ladder
in (2) to a single commutative diagram:
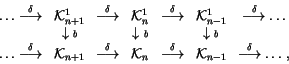 |
(3) |
In this language, Stanford's theorem (Theorem 1) says
that all L shapes in the above diagram (compositions
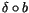 of
``down'' followed by ``right'') are exact.
of
``down'' followed by ``right'') are exact.
Just like singular knots had symbols which were simplar combinatorial
objects (chord diagrams), so do toplogical relators have combinatorial
symbols:
Definition 1.9
Let

,
and let
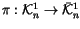
be the projection map.
The following proposition is proved along the same lines as the standard
proof of Proposition 1.6.
Proposition 1.10
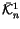
is canonically isomorphic to the space
spanned by all ``relator symbols'', chord diagrams with
n-2 chords and
one
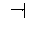
piece corresponding to the special
singularity of Definition
1.8. An example appears in
Figure
7.
Figure 7:
A ``relator symbol''.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...elatorExample.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img72.gif) |
We need to display one additional commutative diagram before we can come to
Hutchings' chain of isomorphisms:
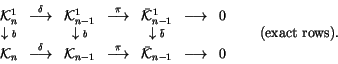 |
(4) |
In this diagram, 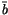 is the ``symbol level'' version of b, and
is induced by
is the ``symbol level'' version of b, and
is induced by
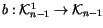 in the usual manner. It
can be described combinatorially by
in the usual manner. It
can be described combinatorially by
Hutchings' chain of isomorphisms is the following chain of equalities and
maps: (here the symbol 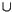 means that the space below is a subspace of
the space above, and the symbol
means that the space below is a subspace of
the space above, and the symbol
 means that the space below is a
sub-quotient of the space above)
means that the space below is a
sub-quotient of the space above)
Theorem 3 (Hutchings [
Hu])
All maps in the above chain are isomorphisms. In particular,
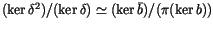
.
Proof. Immediate from diagrams (3)
and (4).

It doesn't look like we've achieved much, but in fact we did, as it
seems that
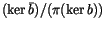 is easier to digest than the
original space of interest,
is easier to digest than the
original space of interest,
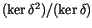 .
The point
is that
.
The point
is that
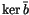 lives fully in the combinatorial realm, being
essentially the space of all relations between 4T relations at the
symbol level. Similarly,
lives fully in the combinatorial realm, being
essentially the space of all relations between 4T relations at the
symbol level. Similarly,
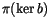 is the space of projections to the
symbol level of relation between 4T relations, and hence we have shown
is the space of projections to the
symbol level of relation between 4T relations, and hence we have shown
Corollary 1.11
Conjecture
1 is equivalent to the
statement ``every relation between 4
T relations at the symbol level has a
lift to the topological level''.
An obvious approach to proving Conjecture 1 thus
emerges:
- Combinatorial step: Find all relations between 4T relations at
the symbols level; that is, find a generating set for
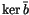 .
.
- For every relation found in the combinatorial step, show that it
lifts to the topological level.
So far, the problem with this approach appears to be in the combinatorial
step. There is a conjectural generating set
 for
for
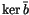 .
Every element in
.
Every element in
 indeed
has a lifting to
indeed
has a lifting to 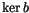 ,
but we still don't know if
,
but we still don't know if
 indeed generates
indeed generates
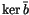 .
We state these facts very briefly; more
information can be found in [Hu] and
in [BS].
.
We state these facts very briefly; more
information can be found in [Hu] and
in [BS].
Definition 1.12
Define

by
As usual, each graphic in the above formula represents a large number of
elements of

,
obtained from the graphic by the addition
of
n-3 chords (first graphic), or
n-5 chords (second graphic), or
n-4 chords (third graphic), or
n-2 chords (fourth graphic). Define
also
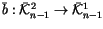
by
A parallel of Conjecture 2 for braids was proven by Hutchings
in [Hu].
Exercise 1.13
Find a space
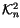
and maps
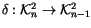
and
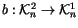
that
fit into a commutative diagram,
and hence show that the relations in
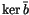
all lift to
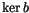
.
Question 1.14
Is the sequence
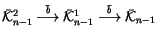
related to Kontsevich's graph
cohomology [
Ko2]?
In summary, we have introduced and studied the following objects, spaces,
and maps:
Objects:
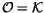 is the space of all framed oriented knots in
an oriented
is the space of all framed oriented knots in
an oriented
 .
More precisely, it is the free
.
More precisely, it is the free
 -module
generated by framed oriented knots in an oriented
-module
generated by framed oriented knots in an oriented
 .
.
The n-Cubes:
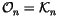 is the free
is the free
 -module generated
by framed oriented knots in an oriented
-module generated
by framed oriented knots in an oriented
 ,
that have
precisely n double point singularities
,
that have
precisely n double point singularities
 as in
Figure 2, modulo the co-differentiability relation
of Definition 1.2,
as in
Figure 2, modulo the co-differentiability relation
of Definition 1.2,
The Co-Derivative: The co-derivative
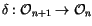 is the map
is the map
 defined by
defined by
The Cube Ladder and Finite
Type Invariants:
The n-Symbols: The space of n-symbols
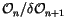 is the space
is the space
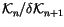 of n-chord diagrams, as in
Figure 3.
of n-chord diagrams, as in
Figure 3.
The Relator Ladder: The relator ladder is the ladder
(see Equation 3), of singular knots with
exactly one ``Topological Relator'' singularity as in
Figure 6.
The Primary
Integrability Constraints: The primary integrability constraints are the images of
the relators via the map b; that is, they are the Topological 4-Term
relations of Figure 4.
The Relator Symbols and
the Symbol-Level Relations: The relator symbols are diagrams of the kind appearing in
Figure 7.
The Once-Reduced Symbol
Space and Once Integrable Weight Systems:
The Inductive
Problem:
The Lifting Problem:
Generic Symbol-Level
Redundencies:
The Object-Level
Redundencies:
The Redundency
Problem:
2. The General Theory of Finite Type Invariants
TBW.
TBW.
3. The case of integral homology spheres
Definition 3.1
An
n-singular integral homology sphere is a pair
(
M,
L) where
M is an integral homology sphere and
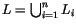
is a unit-framed algebraically split ordered
n-component link
in
M. Namely, the components
Li of
M are numbered 1 to
n(``ordered''), framed with
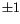
framing (``unit framed''), and the
pairwise linking numbers between the different components of
L are
0 (``algebraically split''). We think of
L as marking
n sites for
performing small modifications of
M, each modification being the surgery
on one of the components of
L. Let us temporarily define
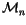
to be the

-module of all formal

-linear combinations of
n-singular integral homology spheres. A correction to the definition of
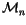
will be given in Definition
3.2 below. Notice that
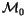
,
which we often simply denote by
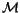
,
is simply the space of
all

-linear combinations of integral homology spheres.
If
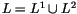 is a framed link (presented as a union of two sublinks
L1 and L2) in some 3-manifold M, we denote by
(M,L1)L2the result of surgery2
of (M,L1) along L2. Namely,
(M,L1)L2 is a pair
(M',L1'),
in which M' is the result of surgery of M along L2, and L1'is the image in M' of L1. Notice that if (M,L) is an
(n+1)-singular integral homology sphere, then
(M,L-Li)Li is again
an n-singular integral homology sphere for any component Li of L.
is a framed link (presented as a union of two sublinks
L1 and L2) in some 3-manifold M, we denote by
(M,L1)L2the result of surgery2
of (M,L1) along L2. Namely,
(M,L1)L2 is a pair
(M',L1'),
in which M' is the result of surgery of M along L2, and L1'is the image in M' of L1. Notice that if (M,L) is an
(n+1)-singular integral homology sphere, then
(M,L-Li)Li is again
an n-singular integral homology sphere for any component Li of L.
We now wish to define the co-derivative map
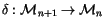 ,
whose adjoint will be the differentiation map for invariants:
,
whose adjoint will be the differentiation map for invariants:
Definition 3.2
Define
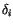
on generators by
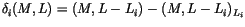
,
and extend it to be a

-linear map
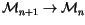
.
For later convinience, we
want to set
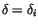
for any
i, but the different
i's may
give different answers. We resolve this by redefining
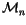
.
Set
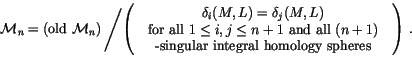 |
(5) |
We can now set (in the new
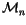
)
The relations in equation (
5) are called ``the
co-differentiability relations''.
We can finally differentiate invariants using the adjoint
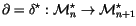 .
That is,
if
.
That is,
if
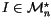 is a differentiable invariant of n-singular
integral homology spheres (namely, which vanishes on the
co-differentiability relations), let its derivative
is a differentiable invariant of n-singular
integral homology spheres (namely, which vanishes on the
co-differentiability relations), let its derivative
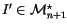 be
be
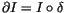 .
Iteratively, one can define multiple
derivatives such us I(k) for any
.
Iteratively, one can define multiple
derivatives such us I(k) for any 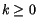 .
.
Definition 3.3
(Ohtsuki [
Oh1]
We say that an invariant
I of integral homology spheres is of type
nif its
n+1st derivative vanishes. We say that it is of finite type if it
is of type
n for some natural number
n.
Unravelling the definitions, we find that I is of type n precisely when
for all integral homology spheres M and all unit-framed algebraically
split (n+1)-component links L in M,
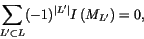 |
(6) |
where the sum runs on all sublinks L' of L (including the empty and
full sublinks), |L'| is the number of components of L', and ML' is
the result of surgery of M along L'. We will not use
equation (6) in this paper.
3.2 Preliminaries
3.2.1 Surgery and the Kirby calculus
Figure 8:
The Left Twist (LT).
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
.../LTDefinition.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img120.gif) |
TBW
3.2.3 The triple linking numbers 
TBW
3.3 Constancy conditions or
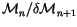
Definition 3.4
Let
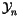
be the unital commutative
algebra over

generated by symbols
Yijk for distinct
indices
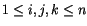
,
modulo the anti-cyclicity relations
Yijk=
Y-1jik=
Yjki.
Warning 3.5
Below we will mostly regard
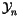
as an

-module, and not as an algebra. Thus we will only use the
product of
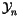
as a convenient way of writing certain elements
and linear combinations of elements. The subspaces of
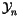
that we
will consider will be subspaces in the linear sense, but not ideals or
subalgebras, and similarly for quotients and maps from or to
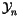
.
It is easy to define a map
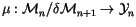 .
For an n-link L set
.
For an n-link L set
It follows from Section 3.2.3 that this definition descends to
the quotient of
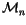 by the co-derivatives of (n+1)-links.
by the co-derivatives of (n+1)-links.
Theorem 4
The thus defined map
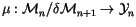
is an isomorphism.
Figure 9:
A 3-mask.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...askDefinition.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img126.gif) |
Figure 10:
The co-derivative of a 3-mask.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...aws/deltaMask.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img127.gif) |
Figure 11:
The Bundle Left Twist (BLT) is the same as the Left Twist, only
that the strands within each ``bundle'' are not twisted internally.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...BLTDefinition.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img128.gif) |
TBW.
3.4 Integrability conditions or
Figure 12:
Undoing a Bundle Left Twist one crossing at a time.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...ws/UndoingBLT.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img129.gif) |
Figure 13:
The Total Twist Relation (TTR).
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...ws/TotalTwist.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img130.gif) |
Figure 14:
The Total Twist Relation (TTR).
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...put draws/TTR.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img131.gif) |
Figure 15:
The Monster
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...draws/Monster.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img132.gif) |
Figure 16:
Lassoing a Borromean link.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...oingBorromean.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img133.gif) |
(The last equality holds because in the two error terms,
YrabYrgb and Yrgb, the component p is unknotted).
Now reduce the component r using the total twist relation. Only the first
term is affected, and 3 of the 6 terms that are produced from its
reduction cancel against the 3 remaining terms of the above equation. The
result is:
The last term here drops out because in it the component r is unknotted,
and so the end result is
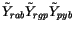 .
In graphical terms,
this is precisely the graph I! Cyclically permuting the roles of r,
g, and b, we find that we have proven the IHX relation.
.
In graphical terms,
this is precisely the graph I! Cyclically permuting the roles of r,
g, and b, we find that we have proven the IHX relation.

An image from http://www.best.com/~abacus/oro/ouroboros.html.
4. The class of Knotted Objects

TBW
TBW
TBW
5. The class of 3-Manifolds
6. The class of Plane Curves
-
- B-N1
- D. Bar-Natan,
On the Vassiliev knot invariants,
Topology 34 423-472 (1995).
- B-N2
- ----,
Bibliography of Vassiliev Invariants,
http://www.math.toronto.edu/~drorbn/VasBib.
- BS
- ---- and A. Stoimenow,
The fundamental theorem of Vassiliev invariants,
in Proc. of the Århus Conf. Geometry and physics,
(J. E. Andersen, J. Dupont, H. Pedersen, and A. Swann, eds.),
lecture notes in pure and applied mathematics 184 (1997) 101-134,
Marcel Dekker, New-York. See also
q-alg/9702009.
- Bi
- J. S. Birman,
New points of view in knot theory,
Bull. Amer. Math. Soc. 28 (1993) 253-287.
- BL
- ----and X-S. Lin,
Knot polynomials and Vassiliev's invariants,
Inv. Math. 111 (1993) 225-270.
- Ga1
- S. Garoufalidis,
On finite type 3-manifold invariants I,
Jour. of Knot Theory and its Ramifications 5 (1996) 441-462.
- Ga2
- ---- and
N. Habegger,
,
The Alexander polynomial and finite type 3-manifold invariants
to appear in Math. Annalen. See also
q-alg/9708002.
- GL1
- ---- and J. Levine,
On finite type 3-manifold invariants II,
Math. Annalen 306 (1996) 691-718. See also
q-alg/9506012.
- GL2
- ---- and ----,
On finite type 3-manifold invariants IV: comparison of
definitions,
Math. Proc. Cambridge Phil. Soc. 122(2) (1997) 291-300. See also
q-alg/9509028.
- GL3
- ---- and ----,
Finite type 3-manifold invariants, the mapping class group and
blinks,
J. Diff. Geom. 47(2) (1997). See also
q-alg/9712045.
- GO1
- ---- and T. Ohtsuki,
On finite type 3-manifold invariants III: manifold weight
systems,
Topology 37-2 (1998). See also
q-alg/9705004.
- GO2
- ---- and ----,
On finite type 3-manifold invariants V: rational homology
3-spheres,
in Proc. of the Århus Conf. Geometry and physics,
(J. E. Andersen, J. Dupont, H. Pedersen, and A. Swann, eds.),
lecture notes in pure and applied mathematics 184 (1997) 445-457,
Marcel Dekker, New-York.
- Go1
- M. Goussarov,
A new form of the Conway-Jones polynomial of oriented links,
in Topology of manifolds and varieties (O. Viro, editor),
Amer. Math. Soc., Providence 1994, 167-172.
- Go2
- ----,
On n-equivalence of knots and invariants of finite degree,
in Topology of manifolds and varieties (O. Viro, editor),
Amer. Math. Soc., Providence 1994, 173-192.
- Go3
- ----,
Interdependent modifications of links and invariants of finite degree,
Topology 37-3 (1998).
- Hu
- M. Hutchings,
Integration of singular braid invariants and graph cohomology,
Harvard University preprint, April 1995 (revised August 1997).
- Ko1
- M. Kontsevich,
Vassiliev's knot invariants,
Adv. in Sov. Math., 16(2) (1993) 137-150.
- Ko2
- ----,
Feynman diagrams and low-dimensional topology,
First European Congress of Mathematics II 97-121, Birkhäuser
Basel 1994.
- Oh1
- T. Ohtsuki,
Finite type invariants of integral homology 3-spheres,
Jour. of Knot Theory and its Ramifications 5(1) (1996) 101-115.
- St1
- T. Stanford,
Finite type invariants of knots, links, and graphs,
Topology 35-4 (1996).
- Va1
- V. A. Vassiliev,
Cohomology of knot spaces,
Theory of Singularities and its Applications (Providence) (V. I. Arnold,
ed.), Amer. Math. Soc., Providence, 1990.
- Va2
- ----,
Complements of discriminants of smooth maps: topology and
applications,
Trans. of Math. Mono. 98, Amer. Math. Soc., Providence, 1992.
About this Paper...
Revision history:
Finite Type Invariants by the Species
This document was generated using the
LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -html_version 3.2 -dir l2h -split 0 -long_titles 4 -show_section_numbers -no_navigation -no_auto_link -no_footnode LongSpecies.tex.
The translation was initiated by Dror Bar-Natan on 2000-03-19
Footnotes
- ... ``classification''1
-
classification (klàs´e-f
 -k
-k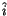 ´shen), in biology,
the systematic categorization of organisms. One aim of modern
classification, or systematics, is to show the evolutionary
relationships among organisms. The broadest division of organisms
is into kingdoms, traditionally two-Animalia (animals) and Plantae
(plants). Widely accepted today are three additional kingdoms:
the Protista, comprising protozoans and some unicellular algae;
the Monera, bacteria and blue-green algae; and the Fungi. From
most to least inclusive, kingdoms are divided into the following
categories: phylum (usually called division in botany), class, order,
family, genus, and species. The species, the fundamental unit of
classification, consists of populations of genetically similar,
interbreeding or potentially interbreeding individuals that share
the same gene pool (collection of inherited characteristics whose
combination is unique to the species). Copyright ©1995
by Columbia University Press. All rights reserved.
´shen), in biology,
the systematic categorization of organisms. One aim of modern
classification, or systematics, is to show the evolutionary
relationships among organisms. The broadest division of organisms
is into kingdoms, traditionally two-Animalia (animals) and Plantae
(plants). Widely accepted today are three additional kingdoms:
the Protista, comprising protozoans and some unicellular algae;
the Monera, bacteria and blue-green algae; and the Fungi. From
most to least inclusive, kingdoms are divided into the following
categories: phylum (usually called division in botany), class, order,
family, genus, and species. The species, the fundamental unit of
classification, consists of populations of genetically similar,
interbreeding or potentially interbreeding individuals that share
the same gene pool (collection of inherited characteristics whose
combination is unique to the species). Copyright ©1995
by Columbia University Press. All rights reserved.
- ... surgery2
-
We recall some basic facts about surgery in
Section 3.2.1.
Dror Bar-Natan
2000-03-19
version exists in a SPLIT edition (about 27 html files and 152 images) for easier browsing, in a LONG edition (one html file, about 152 images) for easier searching and printing, and in a TAR.GZ version (194Kb) for offline browsing.
![]() for some
for some
![]() and
and
![]() is by definition
the difference of the values of V on two ``neighboring'' n-singular
knots, in harmony with the usual definition of derivative for functions
on
is by definition
the difference of the values of V on two ``neighboring'' n-singular
knots, in harmony with the usual definition of derivative for functions
on
![]() .
.
![]() ,
then
,
then
![]() (``W is a constant''). Glancing
at (2), we see that W descends to a linear functional,
also called W, on
(``W is a constant''). Glancing
at (2), we see that W descends to a linear functional,
also called W, on
![]() :
:
![]() has
to satisfy in order to be
has
to satisfy in order to be
![]() for some invariant V. A first
condition is that W must be ``integrable once''; namely, there has to
be some
for some invariant V. A first
condition is that W must be ``integrable once''; namely, there has to
be some
![]() with
with
![]() .
Another quick
glance at (2), and we see that W is integrable once iff
it vanishes on
.
Another quick
glance at (2), and we see that W is integrable once iff
it vanishes on
![]() ,
which is the same as requiring that Wdescends to
,
which is the same as requiring that Wdescends to
![]() (there should be no confusion
regarding the identities of the
(there should be no confusion
regarding the identities of the ![]() 's involved). Often elements of
's involved). Often elements of
![]() are refered to as ``weight systems''. A more accurate
name would be ``once-integrable weight systems''.
are refered to as ``weight systems''. A more accurate
name would be ``once-integrable weight systems''.
![]() .
In
Figure 4 we show a family of members of
.
In
Figure 4 we show a family of members of
![]() ,
the
``Topological 4-Term'' (T4T) relations. Figure 5 explains
how they arise from ``lassoing a singular point''. The following theorem
says that this is all:
,
the
``Topological 4-Term'' (T4T) relations. Figure 5 explains
how they arise from ``lassoing a singular point''. The following theorem
says that this is all:
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...put draws/T4T.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img45.gif)
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...t draws/Lasso.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img46.gif)
![]() :
(see
e.g. [B-N1])
:
(see
e.g. [B-N1])
![\begin{displaymath}4T:\qquad
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
\rai...
...ox{-8pt}{ \input draws/4T.tex }
\hspace{-1.9mm}
\end{array}. \end{displaymath}](img48.gif)
![]() ,
as usual in the theory of finite type invariants of knots.
,
as usual in the theory of finite type invariants of knots.
![]() is a linear functional on
is a linear functional on
![]() .
A question arises
whether every linear functional on
.
A question arises
whether every linear functional on
![]() arises in this way. At least
if the ground ring is extended to
arises in this way. At least
if the ground ring is extended to
![]() ,
the answer is positive:
,
the answer is positive:
![]() ,
we know that we can integrate
once and find
,
we know that we can integrate
once and find
![]() so that
so that
![]() .
Can
we work a bit harder, and find a ``good'' W1, so that there would
be a
.
Can
we work a bit harder, and find a ``good'' W1, so that there would
be a
![]() with
with
![]() ? Proceeding like
that and assuming that all goes well along the way, we would end with a
? Proceeding like
that and assuming that all goes well along the way, we would end with a
![]() with
with
![]() ,
as required. Thus we are
naturally lead to the following conjecture, which implies the Fundamental
Theorem by the backward-inductive argument just sketched:
,
as required. Thus we are
naturally lead to the following conjecture, which implies the Fundamental
Theorem by the backward-inductive argument just sketched:
![]() .
In [Hu],
Michael Hutchings was able to translate the statement
.
In [Hu],
Michael Hutchings was able to translate the statement
![]() to an easier-looking
combinatorial-topological statement, which is implied by
and perhaps equivalent to an even simpler fully combinatorial
statement. Furthermore, Hutchings proved the fully combinatorial statement
in the analogous case of finite type braid invariants, thus proving
Conjecture 1 and Theorem 2
(over
to an easier-looking
combinatorial-topological statement, which is implied by
and perhaps equivalent to an even simpler fully combinatorial
statement. Furthermore, Hutchings proved the fully combinatorial statement
in the analogous case of finite type braid invariants, thus proving
Conjecture 1 and Theorem 2
(over
![]() )
in that case, and thus proving the viability of his
technique.
)
in that case, and thus proving the viability of his
technique.
![]() to something more manageable. Our next step
will be to introduce all the spaces participating in Hutchings' chain.
First, let us consider the space of all T4T relations:
to something more manageable. Our next step
will be to introduce all the spaces participating in Hutchings' chain.
First, let us consider the space of all T4T relations:
![]() form a ladder similar to the one
in (2), and, in fact, they combine with the ladder
in (2) to a single commutative diagram:
form a ladder similar to the one
in (2), and, in fact, they combine with the ladder
in (2) to a single commutative diagram:
![]() of
``down'' followed by ``right'') are exact.
of
``down'' followed by ``right'') are exact.
![]() is the ``symbol level'' version of b, and
is induced by
is the ``symbol level'' version of b, and
is induced by
![]() in the usual manner. It
can be described combinatorially by
in the usual manner. It
can be described combinatorially by
![\begin{displaymath}\bar{b}:
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
\rais...
...{-8pt}{ \input draws/barb.tex }
\hspace{-1.9mm}
\end{array}. \end{displaymath}](img76.gif)
![]() means that the space below is a subspace of
the space above, and the symbol
means that the space below is a subspace of
the space above, and the symbol
![]() means that the space below is a
sub-quotient of the space above)
means that the space below is a
sub-quotient of the space above)

![]()
![]() is easier to digest than the
original space of interest,
is easier to digest than the
original space of interest,
![]() .
The point
is that
.
The point
is that
![]() lives fully in the combinatorial realm, being
essentially the space of all relations between 4T relations at the
symbol level. Similarly,
lives fully in the combinatorial realm, being
essentially the space of all relations between 4T relations at the
symbol level. Similarly,
![]() is the space of projections to the
symbol level of relation between 4T relations, and hence we have shown
is the space of projections to the
symbol level of relation between 4T relations, and hence we have shown
![]() for
for
![]() .
Every element in
.
Every element in
![]() indeed
has a lifting to
indeed
has a lifting to ![]() ,
but we still don't know if
,
but we still don't know if
![]() indeed generates
indeed generates
![]() .
We state these facts very briefly; more
information can be found in [Hu] and
in [BS].
.
We state these facts very briefly; more
information can be found in [Hu] and
in [BS].
![\begin{eqnarray*}\bar b\left(
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
\ra...
...pt}{ \input draws/bGExample.tex }
\hspace{-1.9mm}
\end{array}.
\end{eqnarray*}](img88.gif)
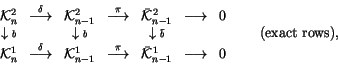
![]() is the space of all framed oriented knots in
an oriented
is the space of all framed oriented knots in
an oriented
![]() .
More precisely, it is the free
.
More precisely, it is the free
![]() -module
generated by framed oriented knots in an oriented
-module
generated by framed oriented knots in an oriented
![]() .
.
![]() is the free
is the free
![]() -module generated
by framed oriented knots in an oriented
-module generated
by framed oriented knots in an oriented
![]() ,
that have
precisely n double point singularities
,
that have
precisely n double point singularities
![]() as in
Figure 2, modulo the co-differentiability relation
of Definition 1.2,
as in
Figure 2, modulo the co-differentiability relation
of Definition 1.2,
![]() is the map
is the map
![]() defined by
defined by
![]() is the space
is the space
![]() of n-chord diagrams, as in
Figure 3.
of n-chord diagrams, as in
Figure 3.
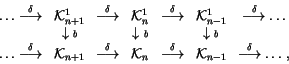
![]() is a framed link (presented as a union of two sublinks
L1 and L2) in some 3-manifold M, we denote by
(M,L1)L2the result of surgery2
of (M,L1) along L2. Namely,
(M,L1)L2 is a pair
(M',L1'),
in which M' is the result of surgery of M along L2, and L1'is the image in M' of L1. Notice that if (M,L) is an
(n+1)-singular integral homology sphere, then
(M,L-Li)Li is again
an n-singular integral homology sphere for any component Li of L.
is a framed link (presented as a union of two sublinks
L1 and L2) in some 3-manifold M, we denote by
(M,L1)L2the result of surgery2
of (M,L1) along L2. Namely,
(M,L1)L2 is a pair
(M',L1'),
in which M' is the result of surgery of M along L2, and L1'is the image in M' of L1. Notice that if (M,L) is an
(n+1)-singular integral homology sphere, then
(M,L-Li)Li is again
an n-singular integral homology sphere for any component Li of L.
![]() ,
whose adjoint will be the differentiation map for invariants:
,
whose adjoint will be the differentiation map for invariants:
![]() .
That is,
if
.
That is,
if
![]() is a differentiable invariant of n-singular
integral homology spheres (namely, which vanishes on the
co-differentiability relations), let its derivative
is a differentiable invariant of n-singular
integral homology spheres (namely, which vanishes on the
co-differentiability relations), let its derivative
![]() be
be
![]() .
Iteratively, one can define multiple
derivatives such us I(k) for any
.
Iteratively, one can define multiple
derivatives such us I(k) for any ![]() .
.
![]() .
For an n-link L set
.
For an n-link L set
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...BLTDefinition.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img128.gif)

