


Next: 1.2 Constancy conditions, ,
Up: 1. The case of
Previous: 1. The case of
As we have already indicated in the introduction, the finite type theory
for knots (Vassiliev theory) is built around the notions of n-singular
knots, and differences between overcrossings and undercrossings. Let us
make those notions precise:
Definition 1.1
An
n-singular knot is an oriented knot in an oriented
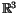
,
which is allowed to have
n singular points that locally look like
the image in Figure
2. For simplicity in the later
parts of this section, we only consider framed (singular or not) knots,
and always use blackboard framing when a knot projection or a part of
a knot projection is drawn.
Figure 2:
A singular point.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...s/DoublePoint.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img11.gif) |
Definition 1.2
Let
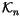
be the

-module freely generated by all
n-singular
knots, modulo the following ``co-differentiability relation'':
Notice that
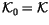
is simply the free

-module generated by
all (framed) knots.
Definition 1.3
Let

be defined by
``resolving'' any one of the singular points in an (
n+1)-singular knot in

:
![\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
\raisebox{8...
...pt}{ \input draws/deltadef.tex }
\hspace{-1.9mm}
\end{array}
\end{displaymath}](img18.gif) |
(1) |
Note that thanks to the co-differentiability relation,
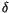
is well
defined. It is called ``the co-derivative''. We denote the adjoint of
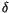
by
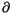
and call it ``the derivative''. It is a map
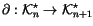
.
The name ``derivative'' is justified by the fact that
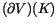 for some
for some
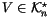 and
and
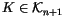 is by definition
the difference of the values of V on two ``neighboring'' n-singular
knots, in harmony with the usual definition of derivative for functions
on
is by definition
the difference of the values of V on two ``neighboring'' n-singular
knots, in harmony with the usual definition of derivative for functions
on
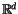 .
.
Definition 1.4
An invariant of knots
V (equivalently, a

-linear functional on
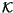
)
is said to be of finite type
n if
its (
n+1)-st derivative vanishes, that is, if
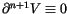
.
(This definition is the analog of one of the standard definitions of
polynomials on
).
When thinking about finite type invariants, it is convenient to have in
mind the following ladders of spaces and their duals, printed here with the
names of some specific elements that we will use later:
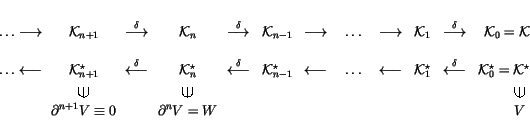 |
(2) |
One may take the definition of a general ``theory of finite type
invariants'' to be the data in (2), with arbitrary
``n-singular objects'' replacing the n-singular knots. Much
of what we will say below depends only on the existance of the
ladders (2), or on the existance of certain natural
extensions thereof, and is therefore quite general.



Next: 1.2 Constancy conditions, ,
Up: 1. The case of
Previous: 1. The case of
Dror Bar-Natan
2000-03-19
![]() for some
for some
![]() and
and
![]() is by definition
the difference of the values of V on two ``neighboring'' n-singular
knots, in harmony with the usual definition of derivative for functions
on
is by definition
the difference of the values of V on two ``neighboring'' n-singular
knots, in harmony with the usual definition of derivative for functions
on
![]() .
.