Dror Bar-Natan and Dylan P. Thurston
Date: This Edition: Jul. 23, 2001; Revision History: Section 6.1.
| Alternative formats |
||||
| Sizes | 232Kb | 144Kb | 464Kb | 728Kb |
Theversion exists in a SPLIT edition (about 32 html files and 151 images) for easier browsing, in a LONG edition (one html file, about 151 images) for easier searching and printing, and in a TAR.GZ version (232Kb) for offline browsing.
Summary. A brief introduction to the fundamental theorem and universal finite type invariants. You can find all that (and more) in [BNS].
The Fundamental Theorem of Finite Type Invariants1 has a deceptively simple formulation and a surprising number of proofs and partial proofs, each one coming with its own philosophy and employing its own set of tools. The purpose of this article is to further study one family of approaches, the algebraic approaches, not so much as to prove the theorem, for this summit is already multiply climbed, but rather for the mere beauty of these specific paths, for the view from some of the vista points along those, for some new perspectives and insights gained along the way, and, well, o.k., also for an occassional technical advantage over the other approaches. In fact, some of the paths we will take don't even make it all the way to the top, or if they do, they are sometimes obviously non-geodetic, but to find the nearby shorter routes one would have to venture a bit into still unexplored territory. So another reason for the existance of this article is to encourage ourselves, and others, to complete and improve what we already have. Thus quoting from the abstract, this article suggests many ``live ends'', unfinished problems that don't seem to be dead ends.
In one form, the Fundamental Theorem of Finite Type Invariants, or just
the Fundamental Theorem throughout this article, asserts that there
exists a universal finite type invariant, an essential invariant
![]() . Let us start by defining the terms
in this statement, and then, in the further parts of this introduction,
we will sketch the algebraic family of approaches (to be followed by
full details in Sections 2-4):
. Let us start by defining the terms
in this statement, and then, in the further parts of this introduction,
we will sketch the algebraic family of approaches (to be followed by
full details in Sections 2-4):
![]()
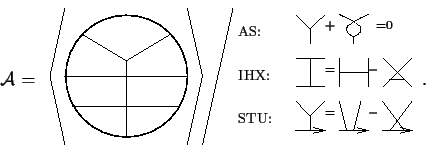
An equivalent formulation of the Fundamental Theorem is that every
degree ![]() weight system is the
weight system is the ![]() th derivative of some type
th derivative of some type ![]() invariant; in particular, it follows that there are lots of finite type
invariants, and it reduces the problem of their enumeration to a finite
algebro-combinatorial problem at any fixed degree.
invariant; in particular, it follows that there are lots of finite type
invariants, and it reduces the problem of their enumeration to a finite
algebro-combinatorial problem at any fixed degree.
Summary. As a toy model for the algebraic approach to the construction of, we give a brief introduction to generators, relations and syzygies in a group-theoretical context, and their use in the construction of group representations.
As we have already mentioned, there are many approaches to the
construction of an invariant
![]() satisfying the condition in Equation (2). The
algebraic approach, which is the topic of this article, is to
find some algebraic context within which the set
satisfying the condition in Equation (2). The
algebraic approach, which is the topic of this article, is to
find some algebraic context within which the set
![]() (or some mild generalization thereof) is finitely presented, and
then to use this finite presentation to define
(or some mild generalization thereof) is finitely presented, and
then to use this finite presentation to define ![]() . Namely, one
would have to make wise guesses
. Namely, one
would have to make wise guesses ![]() for the values of
for the values of ![]() on
the generators
on
the generators ![]() of
of
![]() , so that for each relation
, so that for each relation
![]() the corresponding values of
the corresponding values of ![]() would satisfy the
corresponding relation
would satisfy the
corresponding relation
![]() (two comments: 1. For this
to make sense
(two comments: 1. For this
to make sense
![]() must carry the same kind of algebraic
structure as
must carry the same kind of algebraic
structure as
![]() ; 2. The verification of essentiality,
Equation (2), is typically easy).
; 2. The verification of essentiality,
Equation (2), is typically easy).
Let us see what this entails on a toy model. Suppose we want to
find invariants of elements of the set ![]() of braids on 4 strands.
One way to proceed is to notice that
of braids on 4 strands.
One way to proceed is to notice that ![]() carries an algebraic structure, that is, it has an associative product
which makes it a group. Thus we may seek invariants on
carries an algebraic structure, that is, it has an associative product
which makes it a group. Thus we may seek invariants on ![]() with values
in associative algebras, which respect the algebraic structure. Such
creatures are not new on the mathematical scenery; they are usually called
``group representations''. Our approach to finding representations of
with values
in associative algebras, which respect the algebraic structure. Such
creatures are not new on the mathematical scenery; they are usually called
``group representations''. Our approach to finding representations of
![]() would be to make wise guesses for their values
would be to make wise guesses for their values
![]() ,
,
![]() and
and
![]() on the generators
on the generators ![]() ,
, ![]() and
and ![]() of
of ![]() (see Figure 1), so as to satisfy
the relations between the
(see Figure 1), so as to satisfy
the relations between the ![]() 's. Setting
's. Setting
![]() ,
these relations are (again see Figure 1):
,
these relations are (again see Figure 1):
![\begin{figure}\centering\includegraphics[width=6in]{figs/B4Syzygy.eps}\end{figure}](img39.gif) |
In our real problem, the construction of
![]() , the target space
, the target space
![]() is graded, and we will attempt to construct
is graded, and we will attempt to construct ![]() inductively, degree by
degree. Thus we will be asking ourselves, ``suppose our construction
is done to degree 16; can we extend it to degree 17?''. Let us go back
to the toy model and examine the situation over there. Let
inductively, degree by
degree. Thus we will be asking ourselves, ``suppose our construction
is done to degree 16; can we extend it to degree 17?''. Let us go back
to the toy model and examine the situation over there. Let ![]() be an
associative algebra and let
be an
associative algebra and let
![]() be ideals in
be ideals in ![]() (think ``
(think ``
![]() degrees
degrees![]() and
and
![]() degrees
degrees![]() '')
so that
'')
so that
![]() (``
(``![]() ''). Suppose we have
''). Suppose we have
![]() which satisfy the equations (3) in
which satisfy the equations (3) in ![]() (``done to degree 16''). But equations (3) may fail in
(``done to degree 16''). But equations (3) may fail in
![]() ; let
; let
![]() be the errors in when these
equations are considered in
be the errors in when these
equations are considered in ![]() :
:
We wish to modify the ![]() 's so as to satisfy
equations (3) in
's so as to satisfy
equations (3) in ![]() (``extend to degree
17''), so we set
(``extend to degree
17''), so we set
These are linear equations, and thus to solve our problem, namely to find
![]() 's so that
's so that
![]() , we need to show that the
triple
, we need to show that the
triple
![]() is in the image of the linear map
is in the image of the linear map
![]() defined by
defined by
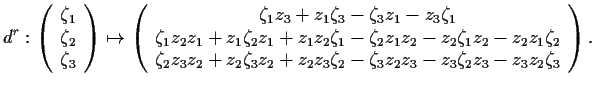
Our strategy to show that
![]() is to find a second linear map
is to find a second linear map
![]() , whose domain is the target space of
, whose domain is the target space of ![]() , so that
, so that
![]() and so that
and so that ![]() . This done we can define the homology group
. This done we can define the homology group
![]() , and if by some magical means we could prove that it vanishes,
we would use
, and if by some magical means we could prove that it vanishes,
we would use ![]() to determine that
to determine that
![]() , and our problem
would be solved. We will mention techniques for the computation of the
homology group
, and our problem
would be solved. We will mention techniques for the computation of the
homology group ![]() in Section 5. For now we only wish
to describe how the map
in Section 5. For now we only wish
to describe how the map ![]() is found.
is found.
To find linear relations between the errors ![]() ,
, ![]() and
and
![]() , we start with a syzygy for our presentation of the braid
group
, we start with a syzygy for our presentation of the braid
group ![]() -- a closed loop whose vertices are words in the generators
-- a closed loop whose vertices are words in the generators
![]() and whose edges are relations. When we perform the replacement
and whose edges are relations. When we perform the replacement
![]() on the vertices of a syzygy, say the one displayed in
Figure 1, we get a loop like such:
on the vertices of a syzygy, say the one displayed in
Figure 1, we get a loop like such:
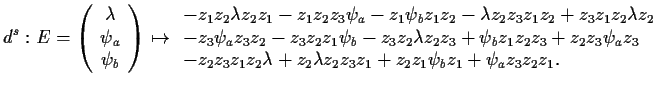
Moral. It would be nice to have an algebraic context within which knot theory is finitely presented and within which the syzygies of the presentation are simple to analyze.
Summary. As an example where the scheme of Section 1.2 has been successfully used, and also in order to display some formulas for later use in this article, we give a very quick reminder of parenthesized tangles and the pentagon and hexagon relations and their syzygies, along the lines of [BN3,BN5,LM].
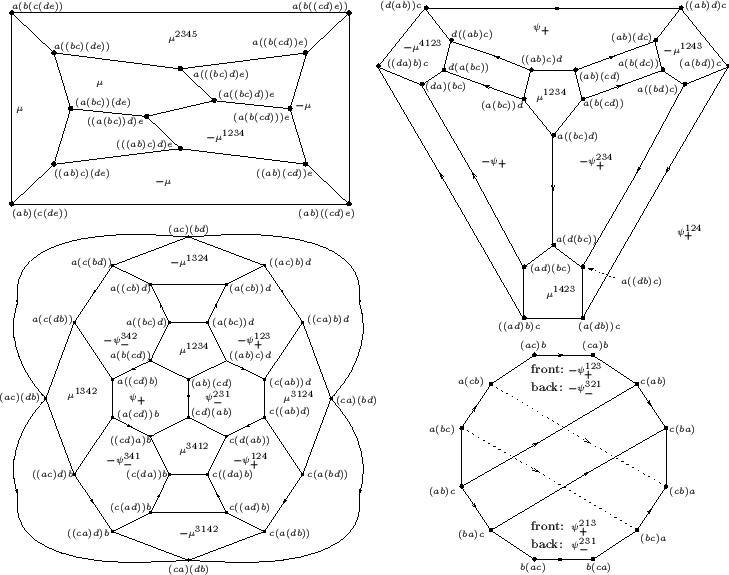
The papers [BN3,BN5,LM] introduce an algebraic context within which the scheme of Section 1.2 is used to construct a universal finite type invariants of links. The ``algebraic context'' there is the structure of a category with certain additional operations. Rather than defining everything in full, we will just recall some key notions, pictures and formulas here.
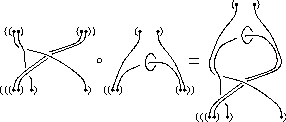 The category
PaT of ``parenthesized tangles'', (the algebraic structure
which we wish to represent, like
The category
PaT of ``parenthesized tangles'', (the algebraic structure
which we wish to represent, like ![]() in
Section 1.2) is the category whose objects are parenthesizations such as
in
Section 1.2) is the category whose objects are parenthesizations such as
![]() or
or
![]() , and whose morphisms are tangles with
parenthesized top and bottom. See the picture on the right, which also
illustrates how parenthesized tangles are composed.
, and whose morphisms are tangles with
parenthesized top and bottom. See the picture on the right, which also
illustrates how parenthesized tangles are composed.
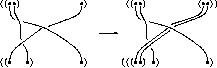 The category
PaT carries some additional
operations. The most interesting are the ``strand addition on the
left/right'' operations, and the strand doubling operations
(illustrated on the right). More details are in [BN3,BN5,LM].
The category
PaT carries some additional
operations. The most interesting are the ``strand addition on the
left/right'' operations, and the strand doubling operations
(illustrated on the right). More details are in [BN3,BN5,LM].
Likewise, one can set up a category
Pa![]() of ``parenthesized chord
diagrams'', that captures the ``symbols'' of ``singular'' parenthesized
tangles as in Equation (1). The category
Pa
of ``parenthesized chord
diagrams'', that captures the ``symbols'' of ``singular'' parenthesized
tangles as in Equation (1). The category
Pa![]() supports the same
additional operations as
PaT, and one may wish to look for structure
preserving functors
supports the same
additional operations as
PaT, and one may wish to look for structure
preserving functors
![]() PaT
PaT![]() Pa
Pa![]() which are ``essential'' in a sense
similar to that of Equation (2).
In [BN3], this is done following the same
generators-relations-syzygies sequence as in
Section 1.2:
which are ``essential'' in a sense
similar to that of Equation (2).
In [BN3], this is done following the same
generators-relations-syzygies sequence as in
Section 1.2:
Now let us assume that we already found ![]() and
and ![]() so that the
relations between them corresponding to
so that the
relations between them corresponding to ![]() and
and
![]() are
satisfied up to degree 16 (say), and let
are
satisfied up to degree 16 (say), and let ![]() and
and ![]() be the degree
17 errors in these equations (compare with Equation (4)).
That is, modulo degrees 18 and up we have (notaion as
in [BN3], compare with [BN3, Equations (10)
and (11)]):
be the degree
17 errors in these equations (compare with Equation (4)).
That is, modulo degrees 18 and up we have (notaion as
in [BN3], compare with [BN3, Equations (10)
and (11)]):
Proceeding as in Equation (5) we set
![]() and
and ![]() with
with ![]() and
and ![]() of
degree 17, and like in Equation (6) we get (compare
with [BN3, Equations (12) and (13)]):
of
degree 17, and like in Equation (6) we get (compare
with [BN3, Equations (12) and (13)]):
Thus we are interested in knowing whether the triple
![]() is
in the image of the linear map
is
in the image of the linear map
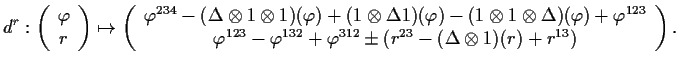
 ; the
symbol
; the
symbol
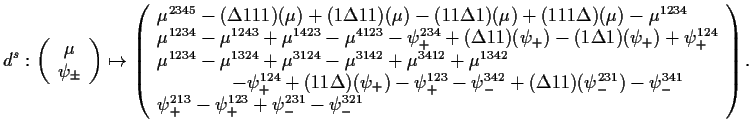
 |
Summary. Here we will define the class of knotted objects we will be working with (knotted trivalent graphs, KTG) and the elementary moves between them. For now, see [BN7, handout].
Summary. Here we will show that with the elementary moves of the previous section, the set KTG is generated by just two of it's elements: the trivially embedded positively twisted Möbius bandand the trivially embedded tetrahedron
. For now, see [BN6, slides 11-16] and [BN7, handout].
Summary. This is the relevant space of chord diagrams for invariants of knotted trivalent graphs. For now, see [MO].
Summary. Here we discuss some relations between the generatorsand
of KTG and show that they are equivalent to Drinfel'd's pentagon and hexagon relations [Dr1,Dr2]. For now, see [BN7, handout].
Summary. Here we will talk about the uniqueness up to vertex renormalizations of a well behaved universal invariant of knotted trivalent. This is the parallel in our theory of the uniqueness up to gauge equivalence of well behaved invariants of q-tangles [LM].
Summary. This is a sticky point. We are quite sure that relative to the elementary moves and with the generatorsand
the set KTG is finitely presented, and we are quite sure that we know all the relations, and they are the pentagon and hexagon of Section 2.4. But depending on our mood in the morning of any given day, we either don't have a proof or are very unhappy about the proof we have. No reference yet.
Summary. Here we will explain how within our contextis related to the theory of
-symbols. A nice Lie algebra problem still remains. No reference yet.
Summary. Our discussion so far implies that if one could set up a well behaved perturbative Chrn-Simons theory (synonymously, a well behaved theory of configuration space integrals), then the invariant of the tetrahedronwould be an associator, when viewed in the right way. We plan a short discussion of this matter here. No reference yet.
Summary. We have some very speculative remarks (that in fact where the origin of this whole study) as for the relationship between everything here and the Witten's Asymptotics Conjecture (that the asymptotics of the Reshetikhin-Turaev invariants is governed by Feynmann-diagram expansions around flat connections) and its sibling the Kashaev-Murakami-Murakami Volume Conjecture. Little as we have to say about it, we'll say it here. For now, see [BN6].
Summary. Another approach for understanding knot theory as a finitely presented theory is within the context of planar algebras which we will review is Section 3.1. Within the context of planar algebras, knot theory has a very nice (and familiar) decription -- it is the theory generated by crossings modulo the standard Reidemeister moves. Even the syzygies of this theory are simply enumerated by codimension two singular plane projections. For now, see [BN8,BN9].
For now, see [J].
Summary. Here we will describe the standard planar algebras of tangles and its associated standard algebra of chord diagrams, and show that there is essential planar algebra map from the former planar algebra to the latter. For now, see [BN9, slide 16].
Summary. There is a ``better'' planar algebra of chord diagrams, that does support a universal finite type invariant. We will define it here. For now, see [BN9, slides 17-18].
Summary. Here is where we will go through the generators-relations-syzygies sequence in the case of the planar algebra of tangles. Nothing's formally written yet.
Summary. This is another semi-successful algebraic approach to the construction of a universal finite type invariants via generators and relations. The central objects here are ``annular braids'', braids in an annulus cross an interval (rather than a disk cross an interval). Nothing written yet.
Summary. Here we will recall the three-step reduction of chord-diagram-valued equations-given-constraints problems into manageable homological algebras problems, as in [Dr2,LM,BN3].
It would be worthwhile for the reader to reflect on the relationship
between the relations and the syzygies of ![]() and singularities of
plane curves. One such codimension one singularity is the triple point
and singularities of
plane curves. One such codimension one singularity is the triple point
![]() , which corresponds
to the last two relations above, which can be viewed as ``the motion of a
double point across a line''. One such codimension two singularity is the
quadruple point
, which corresponds
to the last two relations above, which can be viewed as ``the motion of a
double point across a line''. One such codimension two singularity is the
quadruple point
![]() ,
and it corresponds to the syzygy of Figure 1:
There is a circle-worth of generic deformations of the quadruple
point, corresponding to ``the cross rotating around the target'':
,
and it corresponds to the syzygy of Figure 1:
There is a circle-worth of generic deformations of the quadruple
point, corresponding to ``the cross rotating around the target'':
![]() . The different
codimension one singularities along this rotation are exactly the
relations in our syzygy.
. The different
codimension one singularities along this rotation are exactly the
relations in our syzygy.
Revision History:
This document was generated using the LaTeX2HTML translator Version 99.2beta6 (1.42)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_math -html_version 3.2 -dir l2h -split 0 -long_titles 4 -show_section_numbers -no_navigation -no_auto_link -white -no_footnode LongAlgebraicStructures.tex
The translation was initiated by Dror Bar-Natan on 2001-07-23