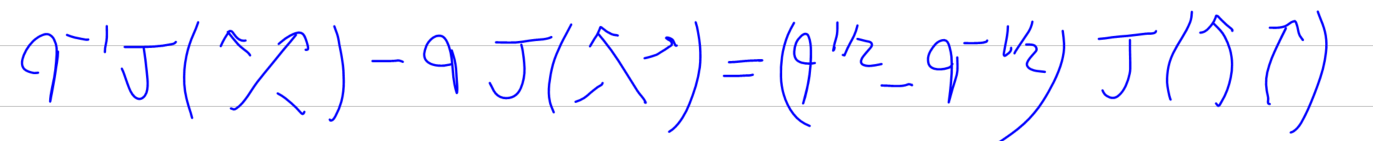
| © | Dror Bar-Natan: Classes: 2021-22: MAT1350F - Algebraic Knot Theory and Computation: | (5) |
Next: On Beyond Zebra!
Previous: About This Class |
Solve and submit the following problems.
Problem 1.
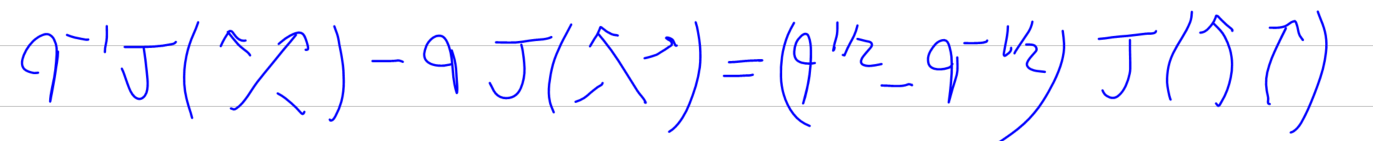
Problem 2. Rather than fixing the Kauffman bracket by using a writhe counter-term, it is tempting to evaluate it at $A=e^{\pi i/3}$, where invariance under R1 holds with no need for a correction. Unfortunately, at $A=e^{\pi i/3}$ the Kauffman bracket of any knot is equal to 1. Prove this.
Problem 3. Prove that the PD notation of a knot diagram determines it as a diagram in $S^2$.
Due date. This assignment is due on Crowdmark by the end of Friday September 24, 2020.