The Axiom of Choice and Zorn's Lemma

Zorn's Lemma. A partially ordered set in which every chain is bounded has a maximal element.

Zorn's Lemma implies the Axiom of Choice. Given a surjection $\pi\colon X\to Y$ let $P=$ $\left\{(B,\beta)\colon B\subset Y,\,\beta\colon B\to X\text{ with }\pi\circ\beta=I_B\right\}$. Declare that $(B_1,\beta_1)\leq(B_2,\beta_2)$ if $B_1\subset B_2$ and $\beta_2\mid_{B_1}=$ $\beta_1$. It is easy to check that $(P,\leq)$ is a partially ordered set. If $C=$ $\{(B_\alpha,\beta_\alpha)\}$ is a chain in $P$, let $B:=$ $\bigcup B_\alpha$ and for any $b\in B$ find some $\alpha$ for which $b\in B_\alpha$ and set $\beta(b)=$ $\beta_\alpha(b)$. Then $\beta$ is well-defined and $(B,\beta)$ is a bound for $C$. Hence by Zorn's lemma, $P$ contains a maximal element $(M,\mu)$. If $M$ is not all of $Y$, add one element to it while extending $\mu$ in an arbitrary manner, contradicting the maximality of $(M,\mu)$. Hence $M=$ $Y$ and we can take $\sigma=$ $\mu$.

For the following proof, a bit of notation: If $Q$ is a partially ordered set and $q\in Q$, we set $Q^{\lt q}:=$ $\{a\in Q\colon a\lt q\}$ and $Q^{\leq q}:=$ $\{a\in Q\colon a\leq q\}$.

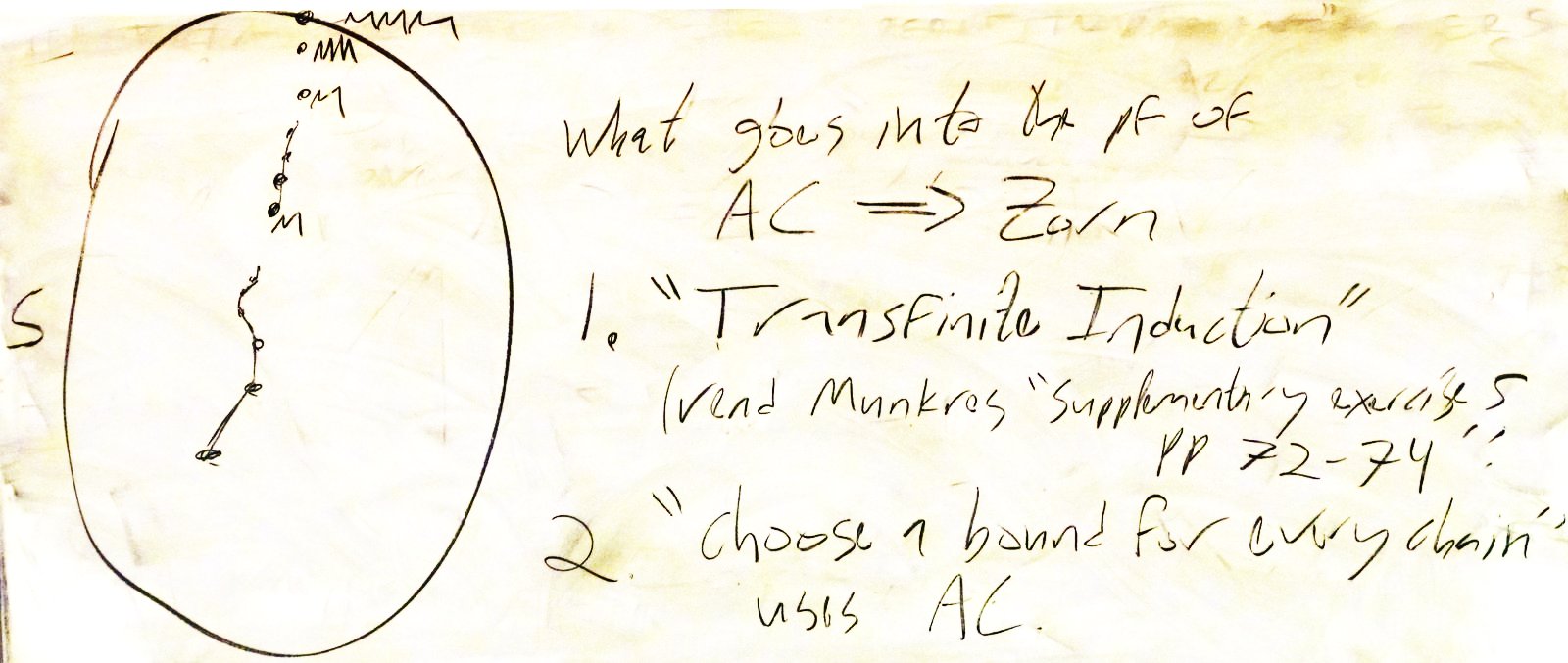
The Axiom of Choice implies Zorn's Lemma. Let $(P,\leq)$ be a partially ordered set in which every chain is bounded, and assume by contradiction that $P$ has no maximal element. This implies that every chain has a strict bound. Use the axiom of choice to pick such a strict bound $M(C)$ for any chain $C$: Namely, for any chain $C\subset P$ (including the empty chain), $M(C)$ is chosen so that $\forall c\in C,\,c\lt M(C)$. This will be the only use of the Axiom of Choice within this proof.

We say that a subset $T\subset P$ is a "tower" if it has the following two properties:

1. $T$ is "well-ordered": every subset of $T$ has a minimal element (relative to the order induced from $P$).
2. $T$ is "inductive": for every $d\in T$, $d=$ $M(T^{\lt d})$.

Lemma. $\calT$ is a chain under $\preceq$.

Proof. Let $T_1$ and $T_2$ be towers, and let $ G:=$ $\{g\in T_1\cap T_2\colon T_1^{\leq g}=$ $ T_2^{\leq g}\}$. If $T_1=$ $G$ then clearly $T_1\preceq T_2$ and we are done. Otherwise, let $b_1$ be the smallest element of $T_1\setminus G$ (it exists as $T_1$ is well-ordered). Now $T_1^{\lt b_1} =$ $ \bigcup\{T_1^{\leq g}\colon g\in T_1,\,g\lt b_1\} =$ $ \bigcup\{T_2^{\leq g}\colon g\in T_1,\,g\lt b_1\}=:$ $H$, where the second equality holds because all the $g$'s appearing in it are in $G$, as they are smaller than $b_1$, the smallest element of $T_1$ which is not in $G$. If $H=$ $T_2$ then $T_2\preceq T_1$ and we are done. Otherwise we reach a contradiction: let $b_2$ be the smallest element of $T_2\setminus H$ (it exists as $T_2$ is well-ordered); it is easy to show that $H=$ $T_2^{\lt b_2}$ and hence $T_1^{\lt b_1}=$ $T_2^{\lt b_2}$. But now by the inductivity of both $T_1$ and $T_2$, $b_1 =$ $ M(T_1^{\lt b_1}) =$ $ M(T_2^{\lt b_2}) =$ $ b_2$, and hence $ T_1^{\leq b_1} =$ $ \{b_1\}\cup T_1^{\lt b_1} =$ $ \{b_2\}\cup T_2^{\lt b_2} =$ $ T_2^{\leq b_2} =$ $T_2^{\leq b_1}$, hence $b_1\in G$, contradicting its choice and completing the proof of the lemma.

Back to the main thread - it is easy to show that the union of a $\preceq$-chain of well-ordered sets is a well-ordered set, and that the union of a $\preceq$-chain of inductive sets is an inductive set and hence the union $\cup\calT$ of all towers in $\calT$ is again a tower, which is hence a maximal tower in $\calT$. But a well-ordered set is in particular a chain (easy), hence $M(\cup\calT)$ makes sense, but then $(\cup\calT)\cup\{M(\cup\calT)\}$ is an even bigger tower in $\calT$, which is a contradiction. This concludes the proof of AC$\Rightarrow$Zorn.

Back to Neptune, the god of the seas, holds an infinite set $H$ of human prisoners on an island in an ocean far away. One day, he assembles the humans and tells them:

Tomorrow I will place a hat on each of you; black or white it will be, and you will not know which it is. You will be able to see all the hats of all other humans, but if any of you will speak or communicate anything with anybody else, I will know, and you will all be doomed. I will then ask you to all call out at the same time the colour of the hat on your heads, and if all but finitely many of you will get it right, you will be set free. Otherwise [evil laughter]. You have until tomorrow to devise a strategy to counter my threat; I so much enjoy seeing humans squirm [more evil laughter]...