Handout for March 29, "Argue by Contradiction" and "Pursue Parity"

Reading. Sections 1.9 and 1.10 of Larson's textbook.

Next Quiz. Thursday March 31, on this handout and those sections.

Problem 1 (Larson's 3.2.17). Let $S$ be a set of primes such that $a,b\in S$ ($a$ and $b$ may be the same) implies that $ab+4\in S$. Prove that $S$ is empty.

Hint. It's nice to work mod 7.

Problem 2 (off topic, but fun). A rectangle is said to be "part whole" if the length of at least one of its sides is a whole number. Prove that if a rectangle $R$ can be partitioned into part whole subrectangles, then $R$ is part whole.

Hint. Consider $\int e^{2\pi i(x+y)}dx\,dy$. (!?!!)

Last year I learned of an article that has 14 proofs of this result! Fourteen Proofs of a Result About Tiling a Rectangle by Stan Wagon, The American Mathematical Monthly 94-7 (1987) 601-617.

Problem 3 (Larson's 1.9.2). In a party with 2016 persons, among any set of four there is at least one person who knows each of the other three. It is also given that there are three people who do not know each other. Prove that the other 2013 people in the party know everyone at the party. (Assume that "knowing" is symmetric. What if not?)

Problem 4 (Larson's 1.10.1, reworded). Given $9$ distinct points in $\bbZ^3$, show that there is some point in $\bbZ^3$ which is exactly half way between two of these $9$ points.

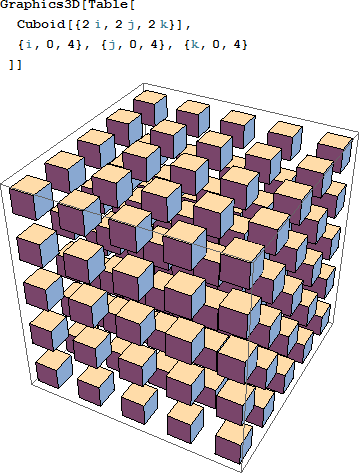
Problem 5.

1. (Larson's 1.10.2, modified). Is there a closed knight-path on a $7\times 7$ chessboard that visits every square of the board exactly once?
2. (An old classic). Removing two opposite corners of an $8\times 8$ chessboard, can you cover what remains with $31$ domino pieces of size $2\times 1$?
3. (A classic variant). Can you cover an $8\times 8$ chessboard with $21$ rectangles of size $3\times 1$ and a single extra $1\times 1$ square?
4. (A 3D variant.) Can you pack 125 boxes of size $4\times 2\times 1$ inside one $10\times 10\times 10$ cube?

Problem 6 (a classic.)

1. Can you draw a quadrilateral (non-convex!) and an additional straight line, such that the straight line cuts through the interior of each of the quadrilateral's edges?
2. Can you draw a pentagon (non-convex!) and an additional straight line, such that the straight line cuts through the interior of each of the pentagon's edges?

Problem 7 (Larson's 1.10.4, reworded). Let $n$ be an odd integer and let $A$ be a symmetric $n\times n$ "Latin" matrix - every row and every column in $A$ is a permutation of $\{1,2,\ldots,n\}$. Show that the diagonal of $A$ is also a permutation of $\{1,2,\ldots,n\}$.

Problem 8 (a classic.) 10 prisoners are made to stand in a line by an evil warden, who also places either a black hat or a white hat on the head of each prisoner. Each prisoner can see all the hats in front of her, but not her own hat or the hats behind her. The evil warden than asks each prisoner for the colour of her hat, starting from the last one who sees all but herself and ending with the first one who sees no one. The prisoners are allowed to make at most one mistake; if they make more than one mistake, they are all executed. If not, they are allowed to participate in the game of Problem 9. Assuming the prisoners know in advance that they will be subject to this game, can they devise a strategy that will allow them to survive at least until the next problem?

Problem 9 (a vicious classic, not for marks.) Our evil warden makes infinitely many prisoners stand in a circle so that each one can see the colour of the hats (black or white) on all heads but herself. All at once, each has to shout the colour of the hat on her head; if only finitely many get it wrong, they are all freed. But if more than just finitely many get it wrong, well, you know what happens in prisoner problems that involve an evil warden. Assuming they had the day before to devise a strategy, can they survive?

Problem 10 (Larson's 1.10.8, reworded). Let $n$ be odd and $\sigma$ a permutation of $\{1,2,\ldots,n\}$. Prove that the product \[ (\sigma_1-1)(\sigma_2-2)\cdots(\sigma_n-n) \] is even.
(And while you're at it, here's a kids' problem. Simplify the expression \[ (a-t)(b-t)(c-t)\cdots(y-t)(z-t) \] as best as you can).

Problem 11 (Larson's 1.10.10, reworded). Show that for every positive integer $a$, the equation $x^2-y^2=a^3$ has solutions with $x,y\in\bbZ$.

Problem 12 (from the $x+y$ movie trailer). $n$ playing cards are placed in a sequence in front of you, some face up and some face down. At any step, you can flip a face up card and any number of cards on its right, no matter which face they are showing. Show that after finitely many steps you will necessarily be facing a sequence of face-down cards.

Problem 13 (Larson's 3.3.20, reworded). Prove that if $n>1$, the sum $1+\frac12+\frac13+\ldots+\frac1n$ is not an integer.
Hint. Multiply by $\operatorname{lcm}(1,2,\ldots,n)$ and consider the parity of the result.