| © | Dror Bar-Natan: Classes: 2015-16: Math 475 - Problem Solving Seminar: | (38) |
Next: Blackboards for Tuesday March 22
Previous: Blackboards for Wednesday March 17 |
Reading. Sections 1.8, 2.6, and 1.9 of Larson's textbook.
Next Quiz. Thursday March 24, on this handout and those sections.
Problem 0 (Dror's addition to Larson's 1.6.2). Of all the $n$-gons with a given perimeter, which has the greatest area?

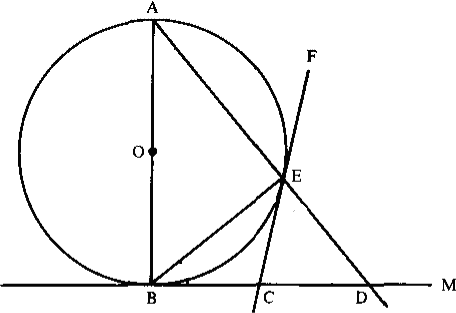
Problem 1 (Larson's 1.8.3). In the figure on the right, everything is as it seems: $O$ is the centre, $AB$ is a diameter, $CE$ and $BC$ are tangents, and all lines are straight. Show that $BC=CD$.
Problem 2 (off topic, but fun). A rectangle is said to be "part whole" if the length of at least one of its sides is a whole number. Prove that if a rectangle $R$ can be partitioned into part whole subrectangles, then $R$ is part whole.
Hint. Consider $\int e^{2\pi i(x+y)}dx\,dy$. (!?!!)
Last year I learned of an article that has 14 proofs of this result! Fourteen Proofs of a Result About Tiling a Rectangle by Stan Wagon, The American Mathematical Monthly 94-7 (1987) 601-617.
Problem 3 (Larson's 2.6.6). If 20 integers are chosen from within the elements of the arithmetic progression 1,4,7,...,100, show that you can find two of them whose sum is 104.
Problem 4 (Larson's 2.6.10, expanded).
Problem 5 (Larson's 2.6.11, abbreviated).
Problem 6 (Larson's 1.9.1). Given that $a$, $b$, and $c$ are odd integers, prove that the equation $ax^2+bx+c=0$ cannot have a rational root.
Problem 7 (Larson's 1.9.2). In a party with 2016 persons, among any set of four there is at least one person who knows each of the other three. It is also given that there are three people who do not know each other. Prove that the other 2013 people in the party know everyone at the party. (Assume that "knowing" is symmetric. What if not?)
Problem 8 (Larson's 1.9.5, abbreviated). A set $S$ of rational numbers is closed under addition and multiplication, and it is given that for every $r\in\bbQ$ exactly one of the following is true: $r\in S$, $-r\in S$, $r=0$. Prove that $S$ is the set of all positive rational numbers.
Problem 9 (Larson's 3.2.1 and 3.2.11, combined) Prove that any subset of size 55 of the set $\{1,2,3,\ldots,100\}$ must contains two numbers differing by 9, 10, 12, and 13, but not does need not contain a pair of numbers differing by 11.
Problem 10 (Larson's 3.2.17). Let $S$ be a set of primes such that $a,b\in S$ ($a$ and $b$ may be the same) implies that $ab+4\in S$. Prove that $S$ is empty.
Hint. It's nice to work mod 7.
Problem 11 (Larson's 5.4.1). Prove that $e=\sum_{k=0}^\infty\frac{1}{k!}$ is an irrational number.
Problem ∞. Which of the 17 tilings patterns appears twice in the picture below?
