\(
\def\bbN{{\mathbb N}}
\def\bbQ{{\mathbb Q}}
\def\bbR{{\mathbb R}}
\def\bbZ{{\mathbb Z}}
\)
Handout for March 8, "Divide into Cases" and "Work Backwards"
Reading. Sections 1.7, 1.8, and 2.6 of Larson's textbook.
Next Quiz. Thursday March 10, on this handout and on sections 1.7 and 1.8.
Problem 1 (Dror's addition to Larson's 1.6.2).
Of all the $n$-gons with a given perimeter, which has the greatest area?
Problem 2 (Larson's 1.7.1). Prove that an angle inscribed in a circle is equal to one half the central angle which subtends the same arc, as in the picture on the right.
Problem 3 (Larson's 1.7.8). Determine $F(x)$, if for all real $x$ and $y$, $F(x)F(y)-F(xy)=x+y$.
Problem 4 (Larson's 2.5.11, modified).
- Let $R_n$ denote the number of ways of placing $n$ nonattacking rooks on an $n\times n$ chessboard so that the resulting arrangement is symmetric about a $90^\circ$ clockwise rotation of the board about
its centre. Compute $R_n$.
- Let $S_n$ denote the number of ways of placing $n$ nonattacking rooks on an $n\times n$ chessboard so that the resulting arrangement is symmetric about the centre of the board. Compute $S_n$.
- Let $T_n$ denote the number of ways of placing $n$ nonattacking rooks on an $n\times n$ chessboard so that the resulting arrangement is symmetric about both diagonals. Compute $T_n$.
Problem 5 (Larson's 2.5.13).
- A derangement is a permutation $\sigma\in S_n$ such that for every $i$, $\sigma i\neq i$. Let $g_n$ be the number of derangements in $S_n$. Show that
\[ g_1=0,\quad g_2=1,\quad g_n=(n-1)(g_{n-1}+g_{n-2}). \]
Hint. A derangement interchanges $1$ with some other element, or not.
- Let $f_n$ be the number of permutations in $S_n$ that have exactly one fixed point (namely, exactly one $i$ such that $\sigma i=i$). Show that $|f_n-g_n|=1$.
Problem 6 (Larson's 1.8.1, modified).
- Let $0<\alpha<\pi$. Show that $\frac{\sin\theta + \sin(\theta+\alpha)}{\cos\theta-\cos(\theta+\alpha)}$ is independent of $\theta$ for $0\leq\theta\leq\alpha$.
- Can you find a geometric interpretation for this fact?
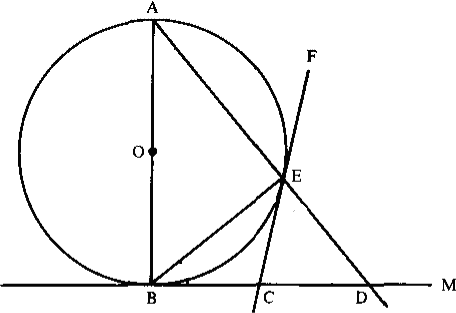
Problem 7 (Larson's 1.8.3). In the figure on the right, everything is as it seems: $O$ is the centre, $AB$ is a diameter, $CE$ and $BC$ are tangents, and all lines are straight. Show that $BC=CD$.
Problem 8. Which of the 17 tilings patterns appears twice in the picture below?