
| © | Dror Bar-Natan: Classes: 2015-16: Math 475 - Problem Solving Seminar: | (18) |
Next: Blackboards for Tuesday February 9
Previous: Blackboards for Thursday February 4 |

Reading. Sections 1.4 and 1.5 of Larson's textbook.
Next Quiz. On Thursday February 11, mostly problems from this handout and from Larson's Sections 1.4 and 1.5.
Problem 0. Put $2^n$ $n$-dimensional oranges of radius $1$ at the corners of the $n$-dimensional cube $[-1,1]^n$, let $B_n$ be the largest blue ball centered at $0$ and bound by these oranges and let $C_n$ be the smallest black cube containing these oranges. Compute \[ \lim_{n\to\infty}\frac{\operatorname{Vol}(B_n)}{\operatorname{Vol}(C_n)} \] (working mathematicians are often shocked by the answer).
Old Problems.
Problem 1 (Larson's 1.4.4). Compute $\displaystyle \int_0^\infty e^{-x^2}dx$.
Problem 2. Compute the volume of the $n$-dimensional sphere $S^n:=\{x\in\bbR^{n+1}\colon|x|=1\}$ in $\bbR^{n+1}$ and the volume of the $n$-dimensional ball $D^n:=\{x\in\bbR^n\colon|x|\leq 1\}$ in $\bbR^n$.
Problem 3 (Larson's 1.5.3). In a triangle $ABC$, $AB=AC$, $D$ is the mid point of $BC$, $E$ is the foot of the perpendicular drawn from $D$ to $AC$, and $F$ is the midpoint of $DE$. Prove that $AF$ is perpendiculr to $BE$. (Hint: use analytic geometry and be clever about the choice of coordinate system).
Problem 4 (Larson's 1.5.4). Let $-1 < a_0 < 1$ and define recursively for $n>0$, \[ a_n=\left(\frac{1+a_{n-1}}{2}\right)^{1/2}. \] What happens to $4^n(1-a_n)$ as $n\rightarrow\infty$?
Problem 5 (Larson's 1.5.6). Guy wires are strung from the top of each of two poles to the base of the other. What is the height from the ground where the two wires cross?
New Problems.
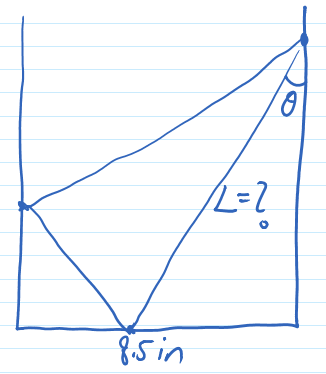
Problem 6 (Larson's 1.5.7). The bottom of this handout (width 8.5in) is folded up and to the left, so that the bottom right corner would align with the left edge of this page. Given the angle of the fold $\theta$, what is the length of the crease $L$? See the figure on the right.
Problem 7 (Larson's 1.5.8). Let $P_1,P_2,\ldots,P_{12}$ be the vertices of a regular 12-gon. Are the diagonals $P_1P_9$, $P_2P_{11}$ and $P_4P_{12}$ concurrent?