The Final Exam and preparing for it

Exam Preparation. Very simply, you should solve everything, and the best for you is if you manage to form study groups to do it together. I will continue holding my normal office hours throughout the examination period until the day of the final (though before coming you are advised to check http://drorbn.net/?title=Office_Hours for possible last-minute changes). In addition, I will have an "open office" the day before the final, on Monday April 20, from 9:30AM until 5PM (excluding washroom and lunch breaks...). You are encouraged to work in the small lounge by my office throughout this period and drop in to ask questions as you please. My office remains at the Bahen building, room 6178.

Some Problems we Skipped

Jan 15 Problem 6 (Larson's 7.1.14). In a convex quadrilateral, prove that the sum of the lengths of the diagonal lies between the perimeter and half the perimeter.

Jan 15 Problem 7 (Larson's 7.4.19). Noting that the function $f(x)=\sqrt{x}$ is concave, show that if $a,b,c$ are positive and satisfy $c>a\cos^2\theta+b\sin^2\theta$, then $\sqrt{c}>\sqrt{a}\cos^2\theta+\sqrt{b}\sin^2\theta$.

Jan 22 Problem 5 (Larson's 1.3.5). On a circle $n$ different points are selected and the chords joining them in pairs are drawn. Assuming no three of these chords pass through the same point, how many intersetion points will there be (inside the circle)?

Jan 22 Problem 6 (Larson's 1.3.6). Given a positive integer $n$, find the number of quadruples of integers $(a,b,c,d)$ such that $0\leq a\leq b\leq c\leq d\leq n$.

Jan 22 Problem 7 (Larson's 1.3.7). The number $5$ can be expressed as a sum of $3$ natural numbers, taking order into account, in $6$ ways: $5=1+1+3=1+2+2=1+3+1=2+1+2=2+2+1=3+1+1$. Let $k\leq n$ be natural numbers. In how many ways can $n$ be written as a sum of $k$ natural numbers, minding the order?

Jan 22 Problem 8. Same as the previous question, but with "natural numbers" replaced with "non-negative integers".

Feb 5 Problem 5 (Larson's 1.6.4). Let $P$ be a point on the graph $G$ of $y=f(x)$, where $f$ is a cubic polynomial. Assume the tangent to the curve at $P$ intersects $G$ again at a point $Q$. Let $A$ be the area bound by $G$ and the segment $PQ$, and let $B$ be the area defined in exactly the same manner, except starting with $Q$ rather than with $P$. What is the relationship between $A$ and $B$?

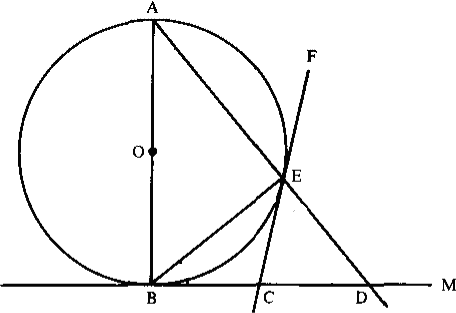
Feb 24 Problem 4 (Larson's 1.8.3). In the figure on the right, everything is as it seems: $O$ is the centre, $AB$ is a diameter, $CE$ and $BC$ are tangents, and all lines are straight. Show that $BC=CD$.

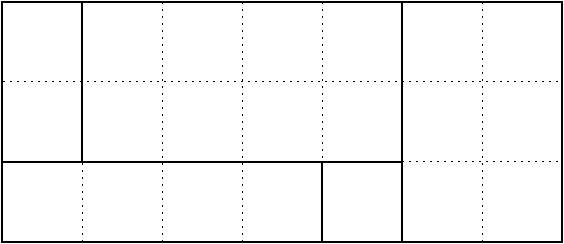
Feb 26 Problem 6 (Larson's 2.6.3, modified). The points on a $3\times 7$ rectangular grid are coloured $Q$ and $M$. Show that you can find a rectangle among these points, whose sides are parallel to the grid axes, and all of whose corners are coloured the same way.

Feb 26 Problem 7 (off topic, but fun). A rectangle is said to be "part whole" if the length of at least one of its sides is a whole number. Prove that if a rectangle $R$ can be partitioned into part whole subrectangles, then $R$ is part whole.

Hint. Consider $\int e^{2\pi i(x+y)}dx\,dy$. (!?!!)

Not so new! I just learned of an article that has 14 proofs of this result! Fourteen Proofs of a Result About Tiling a Rectangle by Stan Wagon, The American Mathematical Monthly 94-7 (1987) 601-617.

Feb 26 Problem 8 (Larson's 2.6.6). If 20 integers are chosen from within the elements of the arithmetic progression 1,4,7,...,100, show that you can find two of them whose sum is 104.

March 5 Problem 10 (Larson's 3.2.1 and 3.2.11, combined) Prove that any subset of size 55 of the set $\{1,2,3,\ldots,100\}$ must contains two numbers differing by 9, 10, 12, and 13, but not need not contain a pair of numbers differing by 11.

March 5 Problem 11 (Larson's 3.2.17). Let $S$ be a set of primes such that $a,b\in S$ ($a$ and $b$ may be the same) implies that $ab+4\in S$. Prove that $S$ is empty.

Hint. It's nice to work mod 7.

March 5 Problem 12 (Larson's 5.4.1). Prove that $e=\sum_{k=0}^\infty\frac{1}{k!}$ is an irrational number.

March 12 Problem 11 (not for marks). Complete your understanding of Ramsey's theorem!

March 19 Problem 1 (Larson's 1.11.1, hinted). Given a finite number of points in the plane, not all of them on the same line, prove that there is a straight line that passes through exactly two of them.

March 19 Problem 8 (Larson's 3.3.28, off topic, modified).

1. Prove that there are infinitely many primes of the form $6n-1$.
   Hint. Consider $(p_1p_2\cdots p_k)^2-1$.
2. Prove that there are infinitely many primes of the form $4n-1$.

March 19 Problem 9. Let $A$ be a subset of $[0,1]$ which is both open and closed, and assume that $0\in A$. Prove that also $1\in A$.