Handout for March 19, "Consider Extreme Cases"

Reading. Section 1.11 of Larson's textbook.

Next Quiz. Thursday March 26 on that section and this handout.

March 12 Problem 2. Can you pack 125 boxes of size $4\times 2\times 1$ inside one $10\times 10\times 10$ cube?

March 12 Problem 3 (a classic.)

1. Can you draw a quadrilateral (non-convex!) and an additional straight line, such that the straight line cuts through the interior of each of the quadrilateral's edges?
2. Can you draw a pentagon (non-convex!) and an additional straight line, such that the straight line cuts through the interior of each of the pentagon's edges?

March 12 Problem 4 (Larson's 1.10.4, reworded). Let $n$ be an odd integer and let $A$ be a symmetric $n\times n$ "Latin" matrix - every row and every column in $A$ is a permutation of $\{1,2,\ldots,n\}$. Show that the diagonal of $A$ is also a permutation of $\{1,2,\ldots,n\}$.

March 12 Problem 6 (a vicious classic, not for marks.) Our evil warden makes infinitely many prisoners stand in a circle so that each one can see the colour of the hats (black or white) on all heads but herself. All at once, each has to shout the colour of the hat on her head; if only finitely many get it wrong, they are all freed. But if more than just finitely many get it wrong, well, you know what happens in prisoner problems that involve an evil warden. Assuming they had the day before to devise a strategy, can they survive?

March 12 Problem 11 (not for marks). Complete your understanding of Ramsey's theorem!

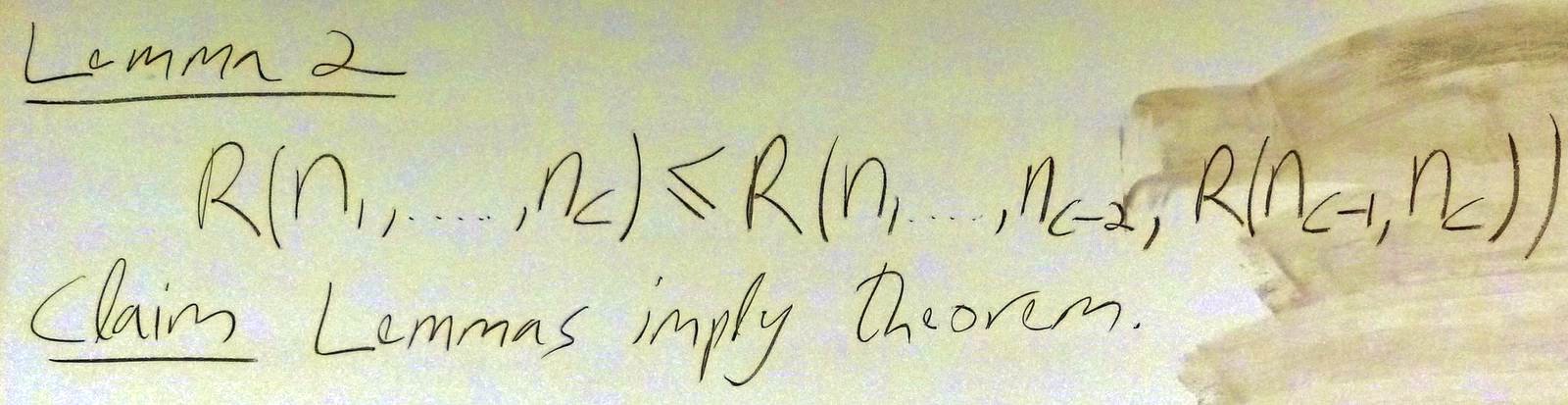
New Problem 1 (Larson's 1.11.1, hinted). Given a finite number of points in the plane, not all of them on the same line, prove that there is a straight line that passes through exactly two of them.
Hint. Consider the triangle with least height whose vertices.

New Problem 2 (Larson's 1.11.2, reworded). Let $A$ be a set of $2n$ points in the plane, no three of them on the same line. Suppose that $n$ of them are coloured red and $n$ are coloured blue. Show that you can choose a pairing of the reds and the blues such the straight line segments between the pairs do not intersect.

New Problem 3 (Larson's 1.11.3). In a party, no boy dances with every girl and each girl dances with at least one boy. Prove that there two couples $bg$ and $b'g'$ which dances, whereas $b$ does not dance with $g'$ and $g$ does not dance with $b'$.

New Problem 4 (Larson's 1.11.4, off topic). Prove that the product of $n$ successive integers is always divisible by $n!$.

New Problem 5 (Larson's 1.11.5). Let $f(x)$ be a polynomial of degree $n$ with real coefficients and such that $f(x)\geq 0$ for every real $x$. Show that $f(x)+f'(x)+\ldots+f^{(n)}(x)\geq 0$ for every real $x$.

New Problem 6 (useful in group theory). Say that a matrix $A$ is ``$\bbZ$-equivalent'' to a matrix $B$ if you can reach from $A$ to $B$ by a sequence of invertible row- and column-operations that involve only integer coefficients (namely, swap two rows, add an integer multiple of one row to another, negate one row, or the same with columns). Show that every matrix $A$ with integer entries is $\bbZ$-equivalent to a diagonal matrix.
Hint. Consider the least of all entries in any matrix $\bbZ$-equivalent to $A$, its row and its column.

New Problem 7 (Larson's 1.11.7). Show that there exists a rational number $c/d$, with $d<100$, such that $\lfloor k\frac{c}{d}\rfloor = \lfloor k\frac{73}{100}\rfloor$ for $k=1,2,\ldots,99$.

New Problem 8 (Larson's 3.3.28, off topic, modified).

1. Prove that there are infinitely many primes of the form $6n-1$.
   Hint. Consider $(p_1p_2\cdots p_k)^2-2$.
2. Prove that there are infinitely many primes of the form $4n-1$.

New Problem 9. Let $A$ be a subset of $[0,1]$ which is both open and closed, and assume that $0\in A$. Prove that also $1\in A$.