| © | Dror Bar-Natan: Classes: 2004-05: Math 157 - Analysis I: | (111) |
Next: Class Notes for Thursday April 7, 2005
Previous: Class Notes for Tuesday April 5, 2005 |
Things we didn't reach.
1. Euler's Formula (aka ``the most beautiful formula in mathematics''):
2. Question. Find a formula for the ![]() 'th term
'th term ![]() in the
sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, etc.
in the
sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, etc.
Hint. It helps to know that
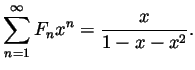
3. Bessel's function ![]() is the solution of the
differential equation
is the solution of the
differential equation
![]() with
with ![]() and
and
![]() . A formula for
. A formula for ![]() is
is
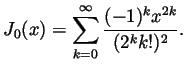
A few things we really have to say.
Definition. We say that a sequence of functions ![]() converges to a function
converges to a function ![]() uniformly on an interval
uniformly on an interval ![]() if for every
if for every
![]() there is some
there is some ![]() so that whenever
so that whenever ![]() and
and ![]() , we have
that
, we have
that
![]() . Likewise we define uniform convergence
for series
. Likewise we define uniform convergence
for series
![]() .
.
Theorem 1. If
![]() uniformly on
uniformly on ![]() and if for
every
and if for
every ![]() the function
the function ![]() is continuous on
is continuous on ![]() , then
, then ![]() is also
continuous on
is also
continuous on ![]() .
.
Theorem 2. If
![]() uniformly on
uniformly on ![]() and if for
every
and if for
every ![]() the function
the function ![]() is integrable on
is integrable on ![]() then
then ![]() is integrable on
is integrable on
![]() and
and
![]() .
.
Theorem 3. A similar though slightly more complicated statement holds for derivatives.
Theorem 4. If the series
![]() is convergent for
some
is convergent for
some ![]() , then it is uniformly and absolutely convergent on
, then it is uniformly and absolutely convergent on
![]() , for every
, for every
![]() . Thus ``all the
good things'' happen for functions such as
. Thus ``all the
good things'' happen for functions such as ![]() .
.
On the Final Exam. It will take place, as dictated by the Higher Authorities, on Wednesday May 4, 7-10PM (late!) at the Upper Small Gymnasium, Benson Building, 320 Huron Street (across from Sidney Smith, south of Harbord Street), Third Floor. The material is very easy to define: Everything. In more details, this is chapters 1-15, 18-20 and 22-24 of Spivak's book, minus appendices plus the appendix to chapter 19 plus some extra material on convexity (as it was discussed in class). If any question will relate to chapter 24, it will be relatively simple and will not require knowing proofs.
Preparing for the Final Exam.
An often-asked question is ``Do we need to know proofs?''. The answer is Absolutely. Proofs are often the deepest form of understanding, and hence they are largely what this class is about. The ones I show in class are precisely those that I think are the most important ones, thus they are the ones you definitely need to know.
Last Comment. Please remember that absolutely all homework is due Friday April 15, 2PM, at the Math Aid Centre.