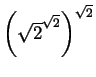 and prove that there are
irrational numbers
and prove that there are
irrational numbers
| © | Dror Bar-Natan: Classes: 2004-05: Math 157 - Analysis I: | (23) |
Next: Math 137's "How to Solve Problems"
Previous: Class Notes for Thursday October 7, 2004 |
Required reading. All of Spivak's Chapter 5.
Recommended for extra practice. From Spivak Chapter 5: 1, 3, 13, 14, 21, 24, 26, 37.
On Term Exam 1. It will take place, as scheduled, during the tutorials on Monday October 18th. You will have an hour and 50 minutes to solve around 5 questions, with no choice questions. The material is everything covered in class until Tuesday October 12th (though not including Thursday October 14th), including everything in the relevant chapters (1-5) of Spivak's book (though not including the appendices to these chapters). Some questions will be taken straight from class, some straight from homework, and some will be fresh. Calculators will be allowed but will not be useful beyond emotional support; no devices that can display text will be allowed. Good luck!
Preparing for Term Exam 1.
An often-asked question is ``Do we need to know proofs?''. The answer is Absolutely. Proofs are often the deepest form of understanding, and hence they are largely what this class is about. The ones I show in class are precisely those that I think are the most important ones, thus they are the ones you definitely need to know.
Just for fun. Stare at the expression
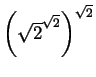 and prove that there are
irrational numbers
and prove that there are
irrational numbers ![]() and
and ![]() so that
so that ![]() is rational. Can you find
specific irrational numbers
is rational. Can you find
specific irrational numbers ![]() and
and ![]() so that
so that ![]() is
rational?
is
rational?
Notice that these are two questions and not one. There is some interesting tale on the philosophy of mathematics for which this is a prime example; have your professor tell you about it some day between XX:00AM and XX:10AM.