© | Dror Bar-Natan: Classes: 2004-05: Math 157 - Analysis I:

(63)

Next: epsilon Previous: Class Notes for Thursday January 6, 2005

Homework Assignment 13

Assigned Tuesday January 11; due Friday January 21, 2PM, at SS 1071

this document in PDF: HW.pdf

Required reading. All of Spivak's chapters 13 and 14.

To be handed in. From Spivak Chapter 14: 1 (odd parts) and 2 (odd parts).

Recommended for extra practice. From Spivak Chapter 14: 1 (even parts) and 2 (even parts).

In class review problem(s) (to be solved in class next Tuesday). Problem 2ii of Spivak Chapter 14: Find the derivative of the following function:

$$F(x)=\int_3^{(\int_1^x\sin^3t dt)}\frac{1}{1+\sin^6t+t^2}dt$$

(if you feel it is necessary, pretend that you've heard of the function $\sin t$ and that $(\sin t)'=\cos t$).

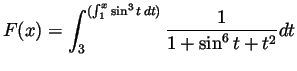
Just for fun. This homework assignment can read your mind!

How does it work? (not on netscape, sorry)

• Think of a two digit number (e.g., 34).
• Subtract from this number its two digits (e.g., 34 - 3 - 4 = 27).
• Find the symbol that corresponds to this number in the table below.
• Concentrate on the symbol and click on the magic square below the table...

(Adopted from http://www.wisecat.vispa.com/mindreader/)

The generation of this document was assisted by L^ATEX2HTML.