Homework Assignment 12a
Assigned Tuesday January 4; due Friday January 14, 2PM,
at
SS 1071
Required reading. All of Spivak's chapter 13
and the web-only handout ``What Went Wrong with
Term Exam 2?''.
My main decisions after reading your comments and some reflection --
- I will try to begin every class asking you ``have you reviewed
your class notes from last class?'', hoping that after some repetitions
of this ritual more of you will take the time for such reviews.
- Almost every homework assignment will have one or two exercises
marked as ``in class review problem(s)''. These will be assigned on
Tuesdays (with the rest of the assignment) and will be solved in class
the following Thursday, two days later. The idea is to get you exposed
to a little more problem solving, and to give you a couple days to
think about these problems before the solution will be presented.
- I will ask the TAs to solve old term exams in the tutorials right
before our two remaining term exams.
- I will take extra care in writing the remaining exams, though I
cannot promise that they will be easier.
- I will aim to cover about 2 weeks worth of material less than
what was covered less year. This will be done by leaving out certain
topics and by thinning the discussion of certain other topics. The
math department undergraduate office will be notified of this change so
that your professors next year will be aware of it too.
- As a first pause (and as HW ran a bit ahead of class), this
homework assignment is identical to the previous one. If you don't
submit it, your grade from the previous one will carry over to this
one. But you also get a chance to do a lot better. Take it!
To be handed in. From Spivak Chapter 13:
Problems 1, 7 (even parts), 8 (even parts), 13 and 37.
Recommended for extra practice. From Spivak
Chapter 13: Problems 5, 7 (odd parts), 8 (odd parts), 9 and 39.
In class review problem(s) (to be solved in
class this Thursday). Problem 15 of Spivak's chapter 13: Prove that
Hint: This can be written
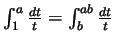 . Every partition
. Every partition
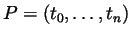 of
of
![$ [1,a]$](img4.gif) gives rise to a partition
gives rise to a partition
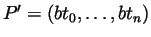 of
of ![$ [b,ab]$](img6.gif) ,
and conversely.
,
and conversely.
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2005-01-03

