| © | Dror Bar-Natan: Classes: 2004-05: Math 157 - Analysis I: | (113) |
Next: Comments on Spivak's Book
Previous: Class Notes for Thursday April 7, 2005 |
Solve the following 6 problems. Each is worth 20 points although they may have unequal difficulty, so the maximal possible total grade is 120 points. Write your answers in the space below the problems and on the front sides of the extra pages; use the back of the pages for scratch paper. Only work appearing on the front side of pages will be graded. Write your name and student number on each page. If you need more paper please ask the presiding officers. This booklet has 12 pages.
Duration. You have 3 hours to write this exam.
Allowed Material: Any calculating device that is not capable of displaying text.
Problem 1.
Problem 2. Sketch the graph of the function
![]() . Make sure that your graph clearly indicates the following:
. Make sure that your graph clearly indicates the following:
Problem 3. Compute the following derivative and the following integrals:
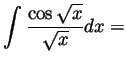
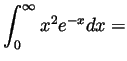
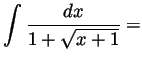
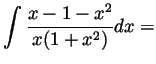
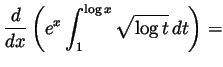
Problem 4. We'll say that a function ![]() is ``bigger''
than a function
is ``bigger''
than a function ![]() (and write
(and write ![]() ) if for every large enough
) if for every large enough
![]() ,
, ![]() . Arrange the following functions by size:
. Arrange the following functions by size:
Problem 5.
Let ![]() be a function which is differentiable
be a function which is differentiable ![]() times at some point
times at some point
![]() .
.
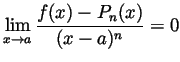 .
.
Problem 6. The ``Cauchy Condensation Theorem'' says
that if a sequence ![]() of positive numbers is decreasing then
of positive numbers is decreasing then
![]() converges iff
converges iff
![]() converges.
converges.
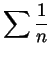 diverges.
diverges.
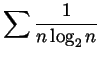 diverges.
diverges.