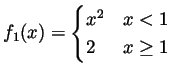 ,
,
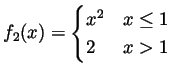 and
and
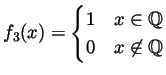 .
.
| Dror Bar-Natan: Classes: 2003-04: Math 157 - Analysis I: | (17) |
Next: JHU's Zucker on Math Courses
Previous: Class Notes for Tuesday September 30, 2003 |
Our task for this week is to master the axiomatically meaningless task of visualization of numbers and functions. We will learn how to interpret graphically all of the following:
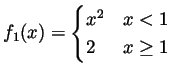 ,
,
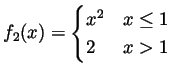 and
and
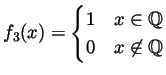 .
.
Just for fun. For ![]() , the number
, the number ![]() is defined to be the result of the following process: Write
is defined to be the result of the following process: Write ![]() in binary,
replace every
in binary,
replace every ![]() in the resulting expansion by a
in the resulting expansion by a ![]() , and interpret the
result as a number written in base 3. For example,
, and interpret the
result as a number written in base 3. For example,
![]() .
.