Dror Bar-Natan: Classes: 2003-04: Math 157 - Analysis I:

(26)

Next: Solution of Term Exam 1 Previous: Class Notes for Thursday October 16, 2003

Term Exam 1

University of Toronto, October 20, 2003

This document in PDF: Exam.pdf

Solve the following 5 problems. Each is worth 20 points although they may have unequal difficulty. Write your answers in the space below the problems and on the front sides of the extra pages; use the back of the pages for scratch paper. Only work appearing on the front side of pages will be graded. Write your name and student number on each page. If you need more paper please ask the tutors. You have an hour and 50 minutes.

Allowed Material: Any calculating device that is not capable of displaying text.

Good Luck!

Problem 1. All that is known about the angle $\alpha$ is that $\tan\frac{\alpha}{2}=\sqrt{2}$. Can you find $\sin\alpha$ and $\cos\alpha$? Explain your reasoning in full detail.

Problem 2.

1. State the definition of the natural numbers.
2. Prove that every natural number $n$ has the property that whenever $m$ is natural, so is $m+n$.

Problem 3. Recall that a function $g$ is called ``even'' if $g(x)=g(-x)$ for all $x$ and ``odd'' if $g(-x)=-g(x)$ for all $x$, and let $f$ be some arbitrary function.

1. Find an even function $E$ and an odd function $O$ so that $f=E+O$.
2. Show that if $f=E_1+O_1=E_2+O_2$ where $E_1$ and $E_2$ are even and $O_1$ and $O_2$ are odd, then $E_1=E_2$ and $O_1=O_2$.

Problem 4. Sketch, to the best of your understanding, the graph of the function

$$f(x)=\frac{1}{x^2-1}.$$

(What happens for $x$ near 0? Near $\pm 1$? For large $x$? Is the graph symmetric? Does it appear to have a peak somewhere?)

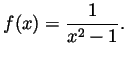
Problem 5.

1. Suppose that $f(x)\leq g(x)$ for all $x$, and that the limits $\lim_{x\to a}f(x)$ and $\lim_{x\to a}g(x)$ both exist. Prove that $\lim_{x\to a}f(x)\leq\lim_{x\to a}g(x)$.
2. Suppose that $f(x)<g(x)$ for all $x$, and that the limits $\lim_{x\to a}f(x)$ and $\lim_{x\to a}g(x)$ both exist. Is it always true that $\lim_{x\to a}f(x)<\lim_{x\to a}g(x)$? (If you think it's always true, write a proof. If you think it isn't always true, provide a counterexample).

The generation of this document was assisted by L^ATEX2HTML.