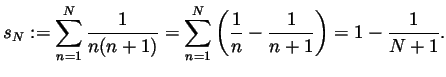Solution of Term Exam 4
Problem and Solution 1. (Graded by Vicentiu Tipu)
Compute the following definite and indefinite integrals in elementary
terms:
-
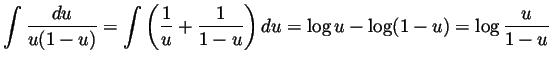 .
.
- With
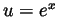 we have
we have 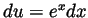 and hence
and hence
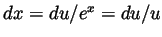 . Thus
. Thus
- With
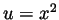 we have
we have 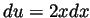 and and when
and and when 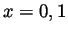 , also
, also 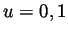 .
Thus
.
Thus
- Using integration by parts with
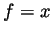 (thus
(thus 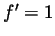 ) and
) and 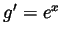 (thus say
(thus say 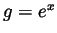 as well), we get
as well), we get
Problem 2. The ``unit ball'' 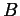 in
in
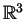 is the result
of revolving the domain
is the result
of revolving the domain
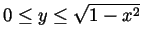 (for
(for
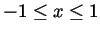 ) around the
) around the 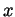 axis.
axis.
- State the general ``Cosmopolitan Integral'' formula for the
volume of a body obtained by revolving a domain bounded under the graph
of a function
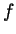 around the
around the 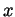 axis.
axis.
- Compute the volume of
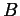 .
.
- State the general ``Cosmopolitan Integral'' formula for the
surface area of a body obtained by revolving a domain bounded under the
graph of a function
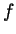 around the
around the 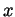 axis.
axis.
- Compute the surface area of
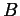 .
.
Solution. (Graded by Cristian Ivanescu)
- The volume
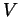 of a body obtained by revolving a domain bounded under
the graph of a function
of a body obtained by revolving a domain bounded under
the graph of a function 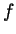 around the
around the 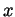 axis, between the vertical
lines
axis, between the vertical
lines 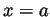 and
and 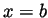 , is
, is
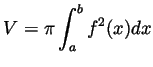 .
.
- Taking
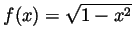 in the above formula we get
in the above formula we get
- The area
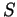 of the surface obtained by revolving the graph of a
function
of the surface obtained by revolving the graph of a
function 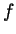 around the
around the 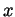 axis, between
axis, between 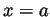 and
and 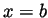 , is
, is
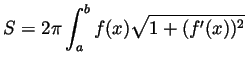 .
.
- Taking
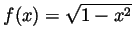 and thus
and thus
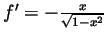 in the above formula we get
in the above formula we get
Problem 3. Let 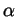 be a real number which is not a
positive integer or 0, let
be a real number which is not a
positive integer or 0, let
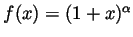 and let
and let 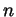 be a positive
integer.
be a positive
integer.
- Compute the Taylor polynomial
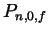 of degree
of degree 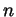 for
for 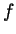 around 0.
around 0.
- Write the corresponding remainder term using one of the formulas
discussed in class.
- Determine (with proof) if there is an interval around 0 on which
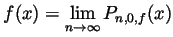 .
.
Solution. (Graded by Julian C.-N. Hung)
-
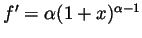 ,
,
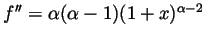 ,
,
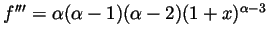 and in general,
and in general,
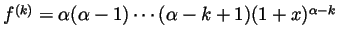 . Thus the Taylor
coefficients are
. Thus the Taylor
coefficients are
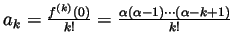 and
so
and
so
- Our first remainder formula says that there is some
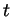 between 0
and
between 0
and 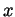 so that (with
so that (with 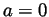 )
)
- The remainder formula above is a product of three factors. The
first in itself is a product of
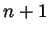 factors of the form
factors of the form
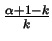 for
for
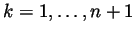 . If
. If
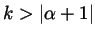 then
then
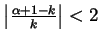 , so the first factor is bounded
by a constant times
, so the first factor is bounded
by a constant times 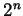 . For any given
. For any given 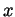 the second factor is
bounded by
the second factor is
bounded by
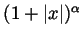 which is independent of
which is independent of 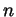 , and if
, and if
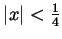 then
then
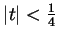 and so
and so
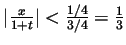 and so the third factor in
the remainder formula is bounded by
and so the third factor in
the remainder formula is bounded by 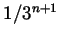 . Multiplying the three
bounds we find that for
. Multiplying the three
bounds we find that for
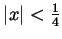 the remainder is bounded by a
constant times
the remainder is bounded by a
constant times 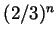 , and this goes to 0 when
, and this goes to 0 when 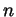 goes to
goes to
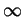 . So at least on the interval
. So at least on the interval
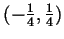 the
remainder goes to 0 and hence
the
remainder goes to 0 and hence
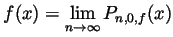 .
.
(Further analysis show that convergence occurs for all
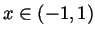 , but
this doesn't concern us here).
, but
this doesn't concern us here).
Problem 4. Let 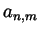 be a ``sequence of sequences''
(an assignment of a real number
be a ``sequence of sequences''
(an assignment of a real number 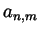 to every pair
to every pair 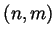 of positive
integers) and assume that
of positive
integers) and assume that 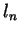 is a sequence so that for every
is a sequence so that for every 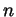 we have
we have
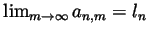 . Further assume that
. Further assume that
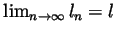 .
.
- Show that for every positive integer
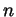 there is a
positive integer
there is a
positive integer 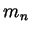
so that
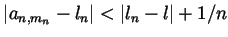 .
.
- Show that
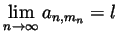 .
.
- (5 points bonus, no partial credit)
Is it always true that also
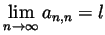 ?
?
Solution. (Graded by Vicentiu Tipu)
- For any fixed
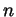 we have that
we have that
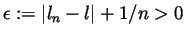 so by the convergence
so by the convergence
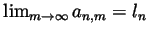 we can find an
we can find an 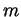 for which
for which
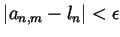 . Rename
. Rename 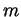 to be
to be 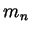 and you are done.
and you are done.
-
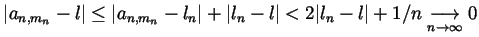 .
.
- Take
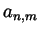 to be the ``identity matrix'':
to be the ``identity matrix'': 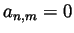 if
if
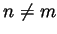 though
though 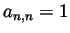 for all
for all 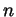 . But then for any fixed
. But then for any fixed 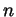 the
sequence
the
sequence 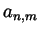 (regarded with
(regarded with 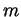 varying) is eventually the constant
0, so
varying) is eventually the constant
0, so
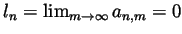 and so
and so
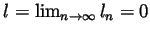 .
But
.
But
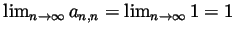 .
.
Problem 5.
- Compute the first 5 partial sums of the series
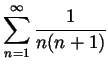 .
.
- Prove that
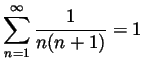 .
.
Solution. (Graded by Cristian Ivanescu)
-
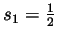 ,
,
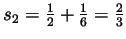 ,
,
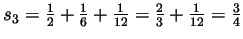 ,
,
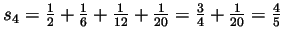 and
and
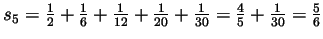 .
.
- Following this trend we guess that
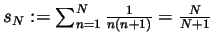 . This we prove by
induction. There is no need to check low
. This we prove by
induction. There is no need to check low 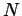 cases -- we've already
done that. So all that remains is
But now,
cases -- we've already
done that. So all that remains is
But now,
Alternative Solution. Note that
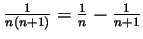 . Then use telescopic summation
to find that
. Then use telescopic summation
to find that
Now continue as at the end of the previous solution.
The results. 79 students took the exam; the average
grade was 62.99, the median was 68 and the standard deviation
was 23.32. The average is thus noticeably below the averages for the
first three term exams, but still higher than last year's average.
I don't know if the same factors from last year applied this time as well;
but for what it's worth, see last year's handout
``What Went Wrong with
Term Exam 4?''.
An unrelated computation.
drorbn@coxeter:~/classes/157AnalysisI:1 math
Mathematica 4.1 for IBM AIX
Copyright 1988-2000 Wolfram Research, Inc.
-- Motif graphics initialized --
In[1]:= D[ArcTan[x], {x, 10}]
9 7 5 3
-185794560 x 371589120 x 243855360 x 58060800 x 3628800 x
Out[1]= ------------- + ------------ - ------------ + ----------- - ---------
2 10 2 9 2 8 2 7 2 6
(1 + x ) (1 + x ) (1 + x ) (1 + x ) (1 + x )
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2004-10-18
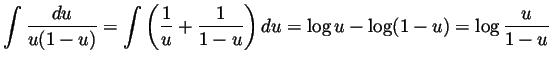 .
.
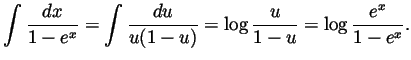
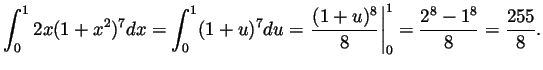
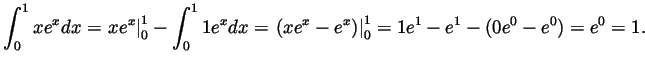
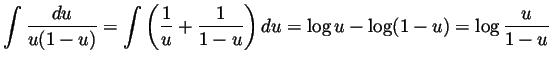 .
.
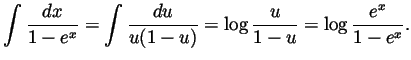
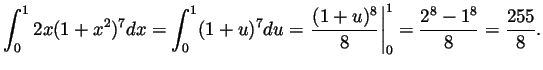
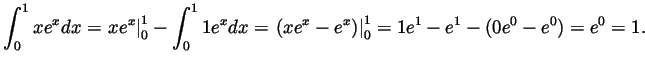
![]() in
in
![]() is the result
of revolving the domain
is the result
of revolving the domain
![]() (for
(for
![]() ) around the
) around the ![]() axis.
axis.
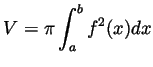 .
.
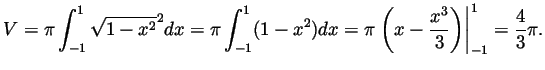
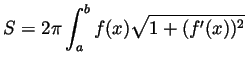 .
.
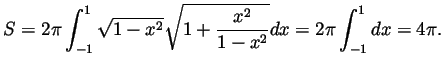
![]() be a real number which is not a
positive integer or 0, let
be a real number which is not a
positive integer or 0, let
![]() and let
and let ![]() be a positive
integer.
be a positive
integer.
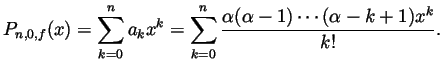
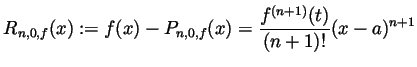
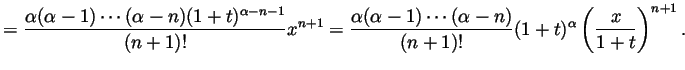
![]() , but
this doesn't concern us here).
, but
this doesn't concern us here).
![]() be a ``sequence of sequences''
(an assignment of a real number
be a ``sequence of sequences''
(an assignment of a real number ![]() to every pair
to every pair ![]() of positive
integers) and assume that
of positive
integers) and assume that ![]() is a sequence so that for every
is a sequence so that for every ![]() we have
we have
![]() . Further assume that
. Further assume that
![]() .
.

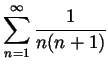 .
.
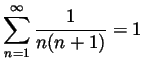 .
.
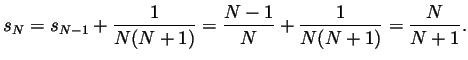
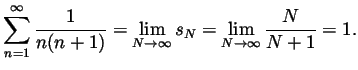
![]() . Then use telescopic summation
to find that
. Then use telescopic summation
to find that