Dror Bar-Natan: Classes: 2003-04: Math 157 - Analysis I:

(52)

Next: Class Notes for Tuesday December 2, 2003 Previous: Term Exam 2

Solution of Term Exam 2

this document in PDF: Solution.pdf

Problem 1. Let $f(x)$ and $g(x)$ be continuous functions defined for all $x$, and assume that $f(0)=g(0)$. Define a new function $h(x)$ by

$$h(x) = \begin{cases} f(x) & x\leq 0, \\ g(x) & x\geq 0. \end{cases}$$

Is $h(x)$ continuous for all $x$? Prove or give a counterexample.

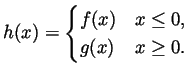
Solution. (Graded by Vicentiu Tipu (red ink) and partially regraded by Dror Bar-Natan (blue/black ink)) Let $\epsilon$ be bigger than 0, and let $a$ be a real number.

• If $a<0$ use the continuity of $f$ at $a$ to find $\delta_2>0$ so that $\vert x-a\vert<\delta_1\Rightarrow\vert f(x)-f(a)\vert<\epsilon$. Set $\delta=\min(-a,\delta_1)$ and then if $\vert x-a\vert<\delta$ then $\vert h(x)-h(a)\vert=\vert f(x)-f(a)\vert<\epsilon$ so $h$ is continuous at $a$.

• If $a>0$ use the continuity of $g$ at $a$ to find $\delta_1>0$ so that $\vert x-a\vert<\delta_1\Rightarrow\vert g(x)-g(a)\vert<\epsilon$. Set $\delta=\min(a,\delta_1)$ and then if $\vert x-a\vert<\delta$ then $\vert h(x)-h(a)\vert=\vert g(x)-g(a)\vert<\epsilon$ so $h$ is continuous at $a$.

• If $a=0$ use the continuity of $g$ at 0 to find $\delta_1>0$ so that $0\leq x<\delta_1\Rightarrow\vert g(x)-g(0)\vert<\epsilon$ and use the continuity of $f$ at 0 to find $\delta_2>0$ so that $-\delta_2<x\leq 0\Rightarrow\vert f(x)-f(0)\vert<\epsilon$. Set $\delta=\min(\delta_1,\delta_2)$. Now if $0\leq x<\delta$ then also $0\leq x<\delta_1$ and hence $\vert h(x)-h(0)\vert=\vert g(x)-g(0)\vert<\epsilon$ and if $-\delta<x\leq 0$ then also $-\delta_2<x\leq 0$ hence $\vert h(x)-h(0)\vert=\vert f(x)-f(0)\vert<\epsilon$. Combining the last two assertions we find that $\vert x\vert<\delta\Rightarrow\vert h(x)-h(0)\vert<\epsilon$, so $h$ is continuous at $a=0$.

Alternative solution for the $a=0$ case: Clearly, by the continuity of $f$ at $a=0$,

$$\lim_{x\to 0^-}h(x)=\lim_{x\to 0^-}f(x)=f(0)=h(0),$$

and by the continuity of $g$ at $a=0$,

$$\lim_{x\to 0^+}h(x)=\lim_{x\to 0^+}g(x)=g(0)=h(0).$$

Thus the two one-sided limits of $h$ exist and are equal (to $h(0)$). By an exercise we did earlier, this implies that $\lim_{x\to 0}h(x)$ also exists and also equals $h(0)$, so $h$ is continuous at $a=0$.

This was not the intended solution -- it's easier than intended and doesn't indicate any understanding of $\epsilon/\delta$ arguments, but the formulation of the question doesn't rule it out, so I had to regrade many exams and give this solution full credit.

Problem 2. We say that a function $f$ is locally bounded on some interval $I$ if for every $x\in I$ there is an $\epsilon>0$ so that $f$ is bounded on $I\cap(x-\epsilon,x+\epsilon)$. Prove that if a function $f$ (continuous or not) is locally bounded on a closed interval $I=[a,b]$ then it is bounded (in the ordinary sense) on that interval.

Hint. Consider the set $A=\{x\in I: f$ is bounded on $[a,x]\}$ and think about P13.

Solution. (Graded by Cristian Ivanescu) Let $A=\{x\in I: f$ is bounded on $[a,x]\}$ as suggested in the hint. $f$ is certainly bounded on $[a,a]$, so $a\in A$, so $A$ is non-empty. Every element of $A$ is in $I$ so is smaller than $b$, so $A$ is bounded by $b$. By P13 $A$ has a least upper bound; call it $c$; clearly $c\leq b$. As $f$ is locally bounded, there is some $\epsilon>0$ so that $f$ is bounded on $[a, a+\epsilon)$ (WLOG, $a+\epsilon<b$) and hence on $[a, a+\frac{\epsilon}{2}]$, so $a+\frac{\epsilon}{2}\in A$, so $c\geq a+\frac{\epsilon}{2}>a$.

Assume by contradiction that $c<b$. Then as $f$ is locally bounded, for some $\epsilon>0$ the function $f$ is bounded by some number $M_1>0$ on $(c-\epsilon,c+\epsilon)$ (WLOG, $c-\epsilon>a$ and $c+\epsilon<b$). As $c$ is a least upper bound, there is some $x\in A$ with $x>c-\epsilon$, and then $f$ is bounded by some other number $M_2>0$ on $[a,x]$. As $[a,x]\cup(x-\epsilon,x+\epsilon)\supset[a,c+\frac{\epsilon}{2}]$, it follows that $f$ is bounded by $\max(M_1,M_2)$ on $[a,c+\frac{\epsilon}{2}]$ and so $c+\frac{\epsilon}{2}\in A$, contradicting the fact that $c$ is an upper bound of $A$. Hence it isn't true that $c<b$, so therefore $c=b$.

Finally, using the fact that $f$ is locally bounded, for some $\epsilon>0$ the function $f$ is bounded by some number $M_1>0$ on $(b-\epsilon,b]$ (WLOG, $b-\epsilon>a$). As $c=b$ is a least upper bound, there is some $x\in A$ with $x>b-\epsilon$, and then $f$ is bounded by some other number $M_2>0$ on $[a,x]$. As $[a,x]\cup(b-\epsilon,b]=[a,b]$, it follows that $f$ is bounded by $\max(M_1,M_2)$ on $[a,b]$, so $f$ is bounded on $[a,b]$ which is what we wanted to prove.

Problem 3.

1. Prove that if a function $g$ satisfies $g'\equiv 0$ on ${\mathbb{R}}$ then $g\equiv c$ for some constant $c$.
2. A certain function $f$ was differentiated twice, and to everybody's surprise, the result was back the function $f$ again, except with the sign reversed: $f''=-f$. It was also found that $f(0)=f'(0)=1$. Set $g(x)=(f(x))^2+(f'(x))^2$ and compute $g'(x)$, $g(0)$ and $g(157)$ (making sure that you explain every step of your computation).

Solution. (Graded by Julian C.-N. Hung)

1. Let $a<b$ be two real numbers. By the mean value theorem there is some $x\in(a,b)$ so that
   $$\frac{f(b)-f(a)}{b-a}=f'(x)=0,$$
   so $f(b)-f(a)=0$ so $f(a)=f(b)$. As $a$ and $b$ were arbitrary, it follows that $f$ is the constant function.

2. $g'(x)=(f^2)'+((f')^2)'=2ff'+2f'(f')'=2ff'+2f'f''=2ff'-2f'f=0$, so $g\equiv c$ for some constant $c$. Now $g(0)=(f(0))^2+(f'(0))^2=1^2+1^2=2$. But $g$ is a constant, so $g(157)$ is also $2$.

Problem 4. Draw a detailed graph of the function

$$f(x)=4\frac{x-1}{x^2}.$$

Your drawing must clearly indicate the domain of definition of $f$, all intersections of the graph of $f$ with the axes, the behaviour of $f$ far out near $\pm\infty$ and near the boundaries of its domain of definition, the regions on which it is increasing or decreasing, the regions on which it is convex or concave and all local and global minima and maxima of $f$.

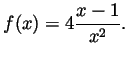
Solution. (Graded by Vicentiu Tipu) $f$ is defined whenever $x^2\neq 0$, so for all $x\neq 0$. If $f(x)=0$ then $x-1=0$ so $x=1$. Near $\pm\infty$,

$$\lim_{x\to\pm\infty}f(x) = \lim_{x\to\pm\infty}\frac{4}{x}-\lim_{x\to\pm\infty}\frac{4}{x^2} = 0.$$

Near $x=0$ the numerator of $f$ goes to $-4$ and the denominator is positive but approaches 0. So $\lim_{x\to 0}f(x)=-\infty$. The derivative is $f'=\frac{8-4x}{x^3}$. This is positive for $0<x<2$ and negative for $x<0$ and for $x>2$, so $f$ is increasing for $0<x<2$ and decreasing for $x<0$ and for $x>2$. At $x=2$ the derivative is 0; before $x=2$ the function is increasing and after $x=2$ it is decreasing, so $f$ has a local maximum at $x=2$. There are no other points in which $f'=0$, so there are no other local maxima and minima. By inspecting the value of $f$ at $x=2$, $f(2)=1$ and comparing it with the behaviour of $f$ at $\pm\infty$ and near 0, we find that $x=2$ is a global maximum. Finally, differentiating a second time we get $f''=8\frac{x-3}{x^4}$. We see that $f''>0$ for $x>3$ and $f''<0$ for $x<3$. So $f$ is convex on $(3,\infty)$ and concave on $(-\infty,0)$ and on $(0,3)$. Summarizing, the graph looks as follows:

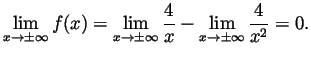
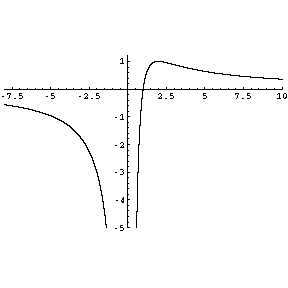
The results. 89 students took the exam; the average grade was 75.1, the median was 76 and the standard deviation was 17.58.

The generation of this document was assisted by L^ATEX2HTML.