| Dror Bar-Natan: Classes: 2003-04: Math 157 - Analysis I: | (76) |
Next: Class Notes for Tuesday February 10, 2004
Previous: Solution of Term Exam 3 |
Required reading. All of Spivak Chapter 19.
To be handed in. From Spivak Chapter 19: Part (vi) of each of problems 1, 2, 3, 5, 7, 9.
Recommended for extra practice. All else in problems 1-9 of Chapter 19. Never finish your work!!! Just get to the point where you are convinced that you know how to continue. In particular, avoid writing what you can do in your head and don't bother to simplify your results.
Just for fun. We all know that
![]() is a very
good approximation to
is a very
good approximation to ![]() ; in fact, it is not difficult to find
people who think that
; in fact, it is not difficult to find
people who think that ![]() is
is
![]() . Prove them wrong,
and also decide which one is bigger (
. Prove them wrong,
and also decide which one is bigger (![]() or
or
![]() ) by
computing the integral
) by
computing the integral
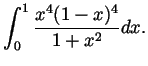
Aside. More on the irrationality of ![]() :
:
Mathematica 4.1 for IBM AIX
Copyright 1988-2000 Wolfram Research, Inc.
-- Motif graphics initialized --
In[1]:= p5 = x^5(a - b x)^5
5 5
Out[1]= x (a - b x)
In[2]:= Expand[p5]/5!
5 5 4 6 3 2 7 2 3 8 4 9 5 10
a x - 5 a b x + 10 a b x - 10 a b x + 5 a b x - b x
Out[2]= ------------------------------------------------------------------
120
In[3]:= derivatives = Table[D[x^7, {x, n}], {n, 0, 10}]
7 6 5 4 3 2
Out[3]= {x , 7 x , 42 x , 210 x , 840 x , 2520 x , 5040 x, 5040, 0, 0, 0}
In[4]:= derivatives /. x -> 0
Out[4]= {0, 0, 0, 0, 0, 0, 0, 5040, 0, 0, 0}