Dror Bar-Natan: Classes: 2003-04: Math 157 - Analysis I:

(114)

Next: Solution of the Final Exam Previous: Last Year's Final Exam Solution

Final Exam

Dror Bar-Natan

April 29, 2004

This document in PDF: Exam.pdf

Solve the following 6 problems. Each is worth 20 points although they may have unequal difficulty, so the maximal possible total grade is 120 points. Write your answers in the space below the problems and on the front sides of the extra pages; use the back of the pages for scratch paper. Only work appearing on the front side of pages will be graded. Write your name and student number on each page. If you need more paper please ask the presiding officers. This booklet has 12 pages.

Duration. You have 3 hours to write this exam.

Allowed Material: Any calculating device that is not capable of displaying text.

Good Luck!

Problem 1. We say that a set $A$ of real numbers is dense if for any open interval $I$, the intersection $A\cap I$ is non-empty.

1. Give an example of a dense set $A$ whose complement $A^c=\{x\in{\mathbb{R}}: x\not\in A\}$ is also dense.
2. Give an example of a non-dense set $B$ whose complement $B^c=\{x\in{\mathbb{R}}: x\not\in B\}$ is also not dense.
3. Prove that if $f\colon{\mathbb{R}}\to{\mathbb{R}}$ is an increasing function ($f(x)<f(y)$ for $x<y$) and if the range $\{f(x): x\in{\mathbb{R}}\}$ of $f$ is dense, then $f$ is continuous.

Problem 2. Sketch the graph of the function $y=f(x)=xe^{-x^2/2}$. Make sure that your graph clearly indicates the following:

• The domain of definition of $f(x)$.
• The behaviour of $f(x)$ near the points where it is not defined (if any) and as $x\to\pm\infty$.
• The exact coordinates of the $x$- and $y$-intercepts and all minimas and maximas of $f(x)$.

Problem 3. Compute the following derivative and the following integrals:

1. $$\frac{d}{dx}\left(\int_0^{\sin x}\sqrt{\arcsin t} dt\right)$$.
2. $$\int\frac{e^{\sqrt{x}}}{\sqrt{x}}dx$$.
3. $$\int x^2e^xdx$$.
4. $$\int\frac{4^xdx}{2^x+1}$$.
5. $$\int\frac{dx}{x^2-3x+2}$$.

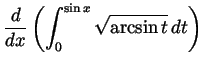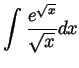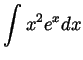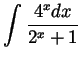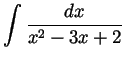Problem 4. In solving this problem you are not allowed to use any properties of the exponential function $e^x$.

1. Two differentiable functions, $e_1(x)$ and $e_2(x)$, defined over the entire real line ${\mathbb{R}}$, are known to satisfy $e_1'(x)=e_1(x)$, $e_2'(x)=e_2(x)$, $e_1(x)>0$ and $e_2(x)>0$ for all $x\in{\mathbb{R}}$ and also $e_1(0)=e_2(0)$. Prove that $e_1$ and $e_2$ are the same. That is, prove that $e_1(x)=e_2(x)$ for all $x\in{\mathbb{R}}$.
2. A differentiable function $e(x)$ defined over the entire real line ${\mathbb{R}}$ is known to satisfy $e'(x)=e(x)$ and $e(x)>0$ for all $x\in{\mathbb{R}}$ and also $e(0)=1$. Prove that $e(x+y)=e(x)e(y)$ for all $x,y\in{\mathbb{R}}$.

Problem 5. In solving this problem you are not allowed to use any properties of the trigonometric functions.

1. A twice-differentiable function $c(x)$ defined over the entire real line ${\mathbb{R}}$ is known to satisfy $c''(x)=-c(x)$ for all $x\in{\mathbb{R}}$ and also $c(0)=c'(0)=0$. Write out the degree $n$ Taylor polynomial $P_{n,a,c}(x)$ of $c$ at $a=0$.
2. Write a formula for the remainder term $R_{n,0,c}(x):=c(x)-P_{n,0,c}(x)$. (To keep the notation simple, you are allowed to assume that $n$ is even or even that $n$ is divisible by 4).
3. Prove that $c$ is the zero function: $c(x)=0$ for all $x\in{\mathbb{R}}$.

Problem 6. In solving this problem you are not allowed to use the irrationality of $\pi$, but you are allowed, indeed advised, to borrow a few lines from the proof of the irrationality of $\pi$.

Is there a non-zero polynomial $p(x)$ defined on the interval $[0,\pi]$ and with values in the interval $[0,\frac12)$ so that it and all of its derivatives are integers at both the point 0 and the point $\pi$? In either case, prove your answer in detail.

The generation of this document was assisted by L^ATEX2HTML.