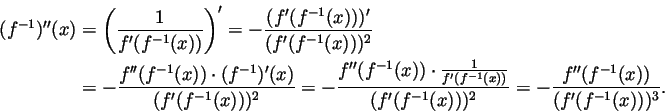Solution of Term Exam 2
Problem 1. Prove that there is a real number 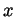 so that
so that
If your proof uses the intermediate value theorem, state it clearly and
prove that it follows from the postulate P13.
Solution. As a composition/sum/quotient of continuous
functions, the left hand side is a continuous function of 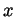 . The
term
. The
term
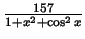 is bounded by 157 and hence the large
is bounded by 157 and hence the large
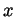 behaviour of the left hand side is dominated by that of
behaviour of the left hand side is dominated by that of 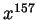 .
Thus for large negative
.
Thus for large negative 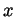 the left hand side goes to
the left hand side goes to  and
for large positive
and
for large positive 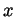 it goes to
it goes to 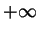 . Thus by the intermediate
value theorem the left hand side must attain the value
. Thus by the intermediate
value theorem the left hand side must attain the value  for some
for some
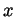 .
.
Our proof does use the intermediate value theorem, and hence its
statement and proof should be reproduced. See Spivak's chapter 8.
Problem 2.
- Define in precise terms ``
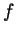 is differentiable at
is differentiable at 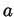 ''.
''.
- Let
Is
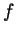 differentiable at 0? If you think it is, prove your assertion
and compute
differentiable at 0? If you think it is, prove your assertion
and compute 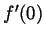 . Otherwise prove that it isn't.
. Otherwise prove that it isn't.
Solution.
- A function
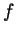 is said to be differentiable at a point
is said to be differentiable at a point 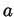 if the
limit
exists.
if the
limit
exists.
- According to the definition of differentiability, we consider the
limit
We claim that this limit is 0 and hence
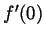 exists and is equal
to 0. Indeed, Let
exists and is equal
to 0. Indeed, Let
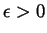 be any positive number and set
be any positive number and set
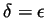 . Now if
. Now if 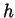 satisfies
satisfies
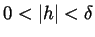 is rational then
is rational then
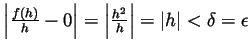 and if
and if 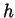 satisfies
satisfies
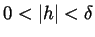 is irrational then
is irrational then
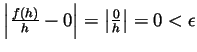 , so
in general
, so
in general
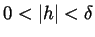 implies
implies
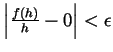 . Thus
. Thus
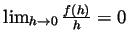 as asserted above.
as asserted above.
Problem 3. Calculate 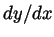 in each of the following
cases. Your
answer may be in terms of
in each of the following
cases. Your
answer may be in terms of 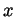 , of
, of 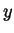 , or of both, but reduce
it algebraically to a reasonably simple form. You do not need
to specify the domain of definition.
, or of both, but reduce
it algebraically to a reasonably simple form. You do not need
to specify the domain of definition.
Solution.
- (a)
- Differentiating both sides with respect to
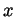 we get
we get
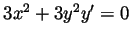 and hence
and hence
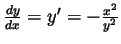 .
.
- (b)
- Using the rule for differentiating a quotient, then the chain
rule and then simplifying a bit, we get
- (c)
- Differentiating both sides with respect to
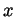 we get
we get
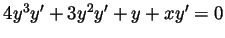 and hence
and hence
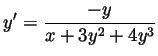 .
.
- (d)
- Using the chain rule,
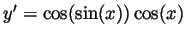 .
.
Problem 4.
- Prove that if
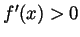 on some interval then
on some interval then 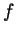 is increasing on
that interval.
is increasing on
that interval.
- Sketch the graph of the function
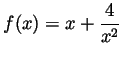 .
.
Solution.
- See Spivak chapter 11.
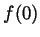 is not defined;
is not defined;
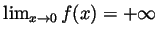 . The only solution
to
. The only solution
to 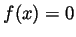 is
is
![$ x=-\sqrt[3]{4}$](Solutionimg41.gif) , so the point
, so the point
![$ (-\sqrt[3]{4}, 0)$](Solutionimg42.gif) is on the
graph.
is on the
graph.
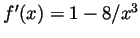 ; this is positive when
; this is positive when
![$ x>\sqrt[3]{8}=2$](Solutionimg44.gif) and when
and when
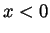 and negative when
and negative when 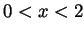 , so
, so 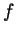 is increasing when
is increasing when
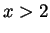 and when
and when
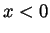 and decreasing when
and decreasing when 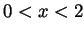 . The derivative is 0 only at
. The derivative is 0 only at
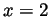 ; right before, the function is decreasing and right after
it is increasing. So
; right before, the function is decreasing and right after
it is increasing. So 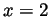 is a local max and we can compute
is a local max and we can compute
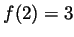 . Finally,
. Finally,
 and near
and near  our
graph
our
graph 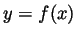 is very close to
is very close to 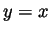 , so we arrive at the following graph:
, so we arrive at the following graph:
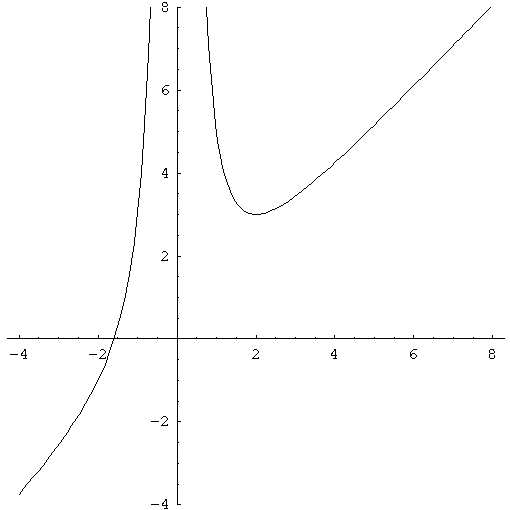
Problem 5. Write a formula for
 in terms of
in terms of
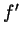 ,
, 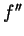 and
and 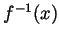 . Under what conditions does your formula hold?
. Under what conditions does your formula hold?
Solution. From class material we knot that if 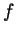 is
continuous and
is
continuous and 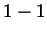 near
near 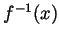 , differentiable at
, differentiable at 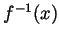 ,
and
,
and
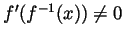 then
then
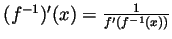 . Using this we get
. Using this we get
In the last chain of equalities we've used the chain rule, for which, in
addition to what we already have, we need to know that 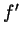 is continuous
around
is continuous
around 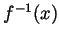 and differentiable at
and differentiable at 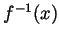 and the rule for
differentiating a quotient, for which we need nothing new. Hence the full
list of conditions needed for aour formula to hold is:
and the rule for
differentiating a quotient, for which we need nothing new. Hence the full
list of conditions needed for aour formula to hold is:
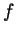 is
is 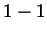 near
near 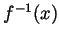 .
.
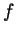 is differentiable around
is differentiable around 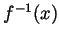 .
.
-
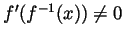 .
.
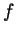 is twice differentiable at
is twice differentiable at 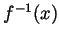 .
.
an alternative solution:

The results. 86 students took the exam; the average grade
is 70.76, the median is 72 and the standard deviation is 18.35.
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2002-12-09
![]() so that
so that

![]() . The
term
. The
term
![]() is bounded by 157 and hence the large
is bounded by 157 and hence the large
![]() behaviour of the left hand side is dominated by that of
behaviour of the left hand side is dominated by that of ![]() .
Thus for large negative
.
Thus for large negative ![]() the left hand side goes to
the left hand side goes to ![]() and
for large positive
and
for large positive ![]() it goes to
it goes to ![]() . Thus by the intermediate
value theorem the left hand side must attain the value
. Thus by the intermediate
value theorem the left hand side must attain the value ![]() for some
for some
![]() .
.
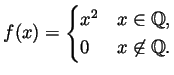
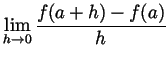
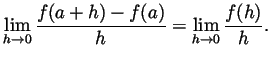
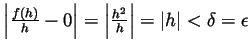 and if
and if 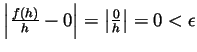 , so
in general
, so
in general
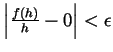 . Thus
. Thus
![]() in each of the following
cases. Your
answer may be in terms of
in each of the following
cases. Your
answer may be in terms of ![]() , of
, of ![]() , or of both, but reduce
it algebraically to a reasonably simple form. You do not need
to specify the domain of definition.
, or of both, but reduce
it algebraically to a reasonably simple form. You do not need
to specify the domain of definition.
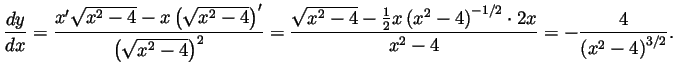
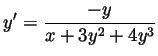 .
.
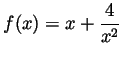 .
.

![]() in terms of
in terms of
![]() ,
, ![]() and
and ![]() . Under what conditions does your formula hold?
. Under what conditions does your formula hold?
![]() is
continuous and
is
continuous and ![]() near
near ![]() , differentiable at
, differentiable at ![]() ,
and
,
and
![]() then
then
![]() . Using this we get
. Using this we get