| Dror Bar-Natan: Classes: 2002-03: Math 157 - Analysis I: | (135) |
Next: Solution of Term Exam 2
Previous: About the Second Term Exam |
Solve the following 5 problems. Each is worth 20 points although they may have unequal difficulty. Write your answers in the space below the problems and on the front sides of the extra pages; use the back of the pages for scratch paper. Only work appearing on the front side of pages will be graded. Write your name and student number on each page. If you need more paper please ask the tutors. You have an hour and 50 minutes.
Allowed Material: Any calculating device that is not capable of displaying text.
Problem 1. Prove that there is a real number ![]() so that
so that
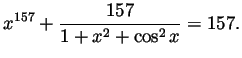
Problem 2.
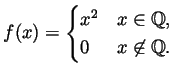
Problem 3. Calculate ![]() in each of the following
cases. Your
answer may be in terms of
in each of the following
cases. Your
answer may be in terms of ![]() , of
, of ![]() , or of both, but reduce
it algebraically to a reasonably simple form. You do not need
to specify the domain of definition.
, or of both, but reduce
it algebraically to a reasonably simple form. You do not need
to specify the domain of definition.
| (c) |
||||
| (d) |
Problem 4.
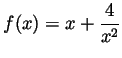 .
.
Problem 5. Write a formula for
![]() in terms of
in terms of
![]() ,
, ![]() and
and ![]() . Under what conditions does your formula hold?
. Under what conditions does your formula hold?