| Dror Bar-Natan: Classes: 2002-03: Math 157 - Analysis I: | (252) |
Next: Homework Assignment 23
Previous: Class Notes for the Week of March 10 (8 of 8) |
Definition.
![]() is ``convergent''
or ``summable'' and
is ``convergent''
or ``summable'' and
![]() if
if
![]() .
Otherwise
.
Otherwise
![]() is ``divergent''.
is ``divergent''.
Claim. When the right hand sides exist, so do the left hand sides and the equalities hold:
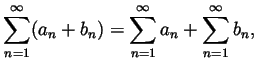
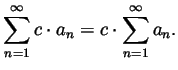
Claim. (The Boundedness Criterion) A nonnegative sequence is summable iff its partial sums are bounded.
Claim. (Cauchy's Criterion) ![]() is summable iff
is summable iff
Claim. (The Vanishing Condition) If ![]() is summable
then
is summable
then ![]() .
.
Theorem 1. (The Comparison Test) If
![]() and
and ![]() converges, then so does
converges, then so does ![]() .
.
Theorem 2. If ![]() and
and ![]() and
and
![]() then
then ![]() converges iff
converges iff ![]() converges.
converges.
Theorem 3. (The Ratio Test) If ![]() and
and
![]() , then
, then ![]() converges if
converges if ![]() and diverges if
and diverges if
![]() .
.
Theorem 4. (The Integral Test) If ![]() and
and ![]() is
decreasing on
is
decreasing on
![]() and
and ![]() , then
, then ![]() converges iff
converges iff
![]() converges.
converges.
Definition.
![]() is ``absolutely
convergent'' if
is ``absolutely
convergent'' if
![]() converges.
converges.
Theorem 5. An absolutely convergent series is convergent. A series is absolutely convergent iff the series formed from its positive terms and its negative terms are both convergent.
Theorem 6. (Leibnitz's Theorem) If ![]() is
non-increasing and
is
non-increasing and
![]() then
then
![]() converges.
converges.
Theorem 7. (skipped) If ![]() converges but not
absolutely, then for any number
converges but not
absolutely, then for any number ![]() there is a rearrangement
there is a rearrangement ![]() of
of
![]() so that
so that
![]() .
.
Theorem 8. If ![]() converges absolutely and
converges absolutely and
![]() is a rearrangement of
is a rearrangement of ![]() , then
, then ![]() also converges
absolutely and
also converges
absolutely and
![]() .
.
Theorem 9. If ![]() and
and ![]() converge
absolutely and the sequence
converge
absolutely and the sequence ![]() is composed of all the products of the
form
is composed of all the products of the
form ![]() , then
, then
![]() .
.