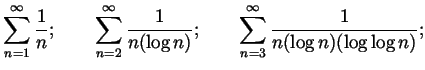
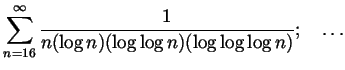
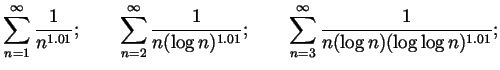
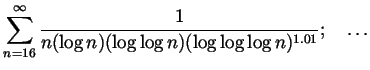
| Dror Bar-Natan: Classes: 2002-03: Math 157 - Analysis I: | (242) |
Next: Eric DeGiuli's Solution of Homework Assignment 22
Previous: Class Notes for the Week of March 3 (6 of 6) |
Required reading. All of Spivak Chapter 23. Also read (but don't do!) all exercises for that chapter -- just to get an impression for how intricate the various convergence tests and criteria can get.
To be handed in. From Spivak Chapter 23: 1 (parts divisible by 4), 12, 23 as well as the following question:
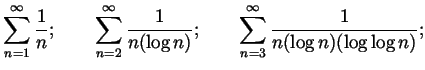
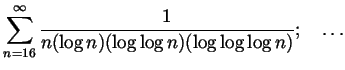
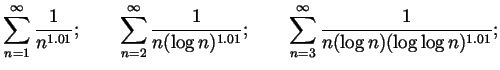
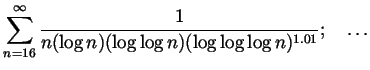
Recommended for extra practice. From Spivak Chapter 23: 1 (the rest), 5, 20, 21 as well as the following question: