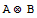
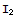
See http://www.math.toronto.edu/~drorbn/Talks/QuantumProbability/UWO-040213.html
We start by loading a necessary Mathematica package, by defininig the tensor product ![]()
![]()
In[1]:=
![]()
In[2]:=
![]()
Next we define the unit "probability vector" v, and our observables ("random variables") ![]() and
and ![]() as tensor products of
as tensor products of ![]() with some prescribed
with some prescribed ![]() :
:
In[3]:=
![]()
In[4]:=
![]()
Out[4]=
![{( Cos[2 α] Sin[2 α] 0 0 ), ( Cos[2 β] 0 ... 2 α] -Cos[2 α] 0 Sin[2 β] 0 -Cos[2 β]](HTMLFiles/index_11.gif)
We check that both ![]() and
and ![]() are (±1)-valued and have zero mean, hence both attain +1 and -1 with 50-50 chance:
are (±1)-valued and have zero mean, hence both attain +1 and -1 with 50-50 chance:
In[5]:=
![]()
Out[5]=
![]()
The ![]() 's and the
's and the ![]() 's commute, hence they have a joint distribution! Indeed,
's commute, hence they have a joint distribution! Indeed,
In[6]:=
![]()
Out[6]=
![]()
The ![]() 's and the
's and the ![]() 's are both (±1)-valued, so the probability that they are equal is the expectation value (mean) of
's are both (±1)-valued, so the probability that they are equal is the expectation value (mean) of ![]() :
:
In[7]:=
![]()
Finally, the following is stricktly impossible, classically speaking:
In[8]:=
![]()
Out[8]=
![{Sin[α - β]^2, ( 3 3 )} - - ... 3 3 - - 4 4 0](HTMLFiles/index_25.gif)
See also N. D. Mermin, Physics Today 39(4) 38 (1985) and D. Bar-Natan, Foundations of Physics 19(1) 97 (1989).
Converted by Mathematica (February 12, 2004)