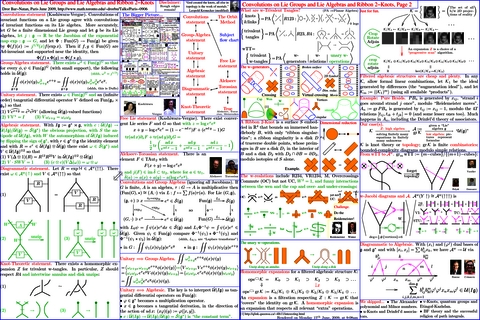
Abstract. I'll start my talk by describing the Kashiwara-Vergne Conjecture (1978, Proven Alekseev-Meinrenken, 2006), which states that for any finite dimensional Lie group, certain convolutions on the group are equal to certain convolutions on its Lie algebra, and I'll end my talk in knot theory. Going backward from the hard to the easy, here's the whole thing in one paragraph:Convolutions are integrals so we need to prove an equality of integrals. This we do (roughly) by finding a Measure Preserving Transformation (MPT) which carries one integrand to the other. This has to work for any Lie group, so the MPT better be given as a universal formula. At this generality all we have to work with is the Lie bracket, and bracket-made formulas can be pictured as certain trivalent diagrams (which in themselves are subject to the Jacobi, or "IHX" relation). Thus we are really seeking a certain big sum V of trivalent diagrams, which, in order to describe our desired MPT, must satisfy certain equations mod IHX. Our space Aw of trivalent diagrams turns out to be the "associated graded" space of the space Kw of ribbon 2-knots in 4-space, and the equations V needs to solve are the equations one needs to solve to get a well-behaved "expansion" Z:Kw-->Aw.
Thus the Kashiwara-Vergne Conjecture, itself a witness to the famed "orbit method", is more or less the same as a natural problem in knot theory, and since knot theory is related to associators and to quantum groups, so is the Kashiwara-Vergne Conjecture. Cool, eh?
Major Handout. KV.html, KV.pdf, KV.png (source files: KV.zip).
Minor Handout. 3x4.html, 3x4.pdf, 3x4.png (source files: 3x4.zip).
Paper in progress. Finite Type Invariants of W-Knotted Objects: From Alexander to Kashiwara and Vergne.
My scratch work. Pensieve/2009-04 (mostly under "Glasgow"), Pensieve/2009-05 (mostly under "Trieste"), and Pensieve/2009-06.

|
|