Expansions

Five Chaire de la Vallée-Poussin talks in Louvain-la-Neuve, Belgium, June 1-5, 2015.

Links: AKT AM AT Bern CS Dal F inf KBH KV mac vX WKO WKO1 WKO2 X ZD

Abstract. It is less well known than it should be, that the standard notion of an expansion of a smooth function on a Euclidean space into a power series ("the Taylor expansion") is vastly more general than it first seems; in fact, it is almost ridiculously more general. In my series of talks I will concentrate on expansions for knotted objects in 3 and 4 dimensions, on how these expansions relate these objects to problems in Lie theory, and on how these expansions may be constructed using tools from quantum field theory (which in themselves are "expansions").

Source Files: pensieve.

Talk I: The Kashiwara-Vergne Problem and Topology. I will describe the general "expansions" machine whose inputs are topics in topology (and more) and whose outputs are problems in algebra. There are many inputs the machine can take, and many outputs it produces, but I will concentrate on just one input/output pair. When fed with a certain class of knotted 2-dimensional objects in 4-dimensional space, it outputs the Kashiwara-Vergne Problem (1978, solved Alekseev-Meinrenken 2006, elucidated Alekseev-Torossian 2008-2011), a problem about convolutions on Lie groups and Lie algebras.

This will be an overview talk: you do not need to know what the Kashiwara-Vergne problem is in order to understand this talk, nor do you have to have seen a 2-knot before, and most details will await further discussion in the later talks.

Handout. Louvain1.html, Louvain1.pdf.
Talk Video.
Papers. WKO1.pdf, WKO2.pdf.

Talk II: From Knots to Lie Algebras. Why on Earth should knots be related to Lie algebras? The former are squishy and irregular, the latter are symmetric and rigid. They should know nothing of each other. Yet as we shall see, the natural target space for expansions for knots is in some sense, "the universal dual" of all (metrized) Lie algebras.

Handout. Louvain2.html, Louvain2.pdf.

Talk Video.

Talk III: Chern-Simons Theory and Feynman Diagrams. We will study Feynman diagrams in ${\mathbb R}^n$ and then apply the techniques we will have learned to the case of the infinite-dimensional Chern-Simons path integral. The result $Z^u$ will be an expansion for knots, or a "universal finite type invariant".

Handout. Louvain3.html, Louvain3.pdf.
The back side. Portfolio.

Talk Video.

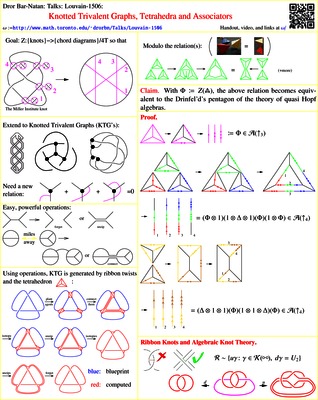
Talk IV: Knotted Trivalent Graphs and Associators. We will find that in order to compute our expansion $Z^u$ on arbitrary knots, it is enough to compute or guess its value on just one specific knotted trivalent graph - the unknotted tetrahedron in ${\mathbb R}^2$. This, it turns out, is precisely what is called "a Drinfel'd associator".

Handout. Louvain4.html, Louvain4.pdf.
The back side. Infrastructure.

Talk Video.

Talk V: Back to 4D. We will repeat the 3D story of the previous 3 talks one dimension up, in 4D. Surprisingly, there's more room in 4D, and things get easier, at least when we restrict our attention to "w-knots", or to "simply-knotted 2-knots". But even then there are intricacies, and we try to go beyond simply-knotted, we are completely confused.

Handout. Louvain5.html, Louvain5.pdf.

Talk Video.