Dror Bar-Natan:
Talks:
Istanbul-0606:
Algebraic Knot Theory Summary
an unproven thesis and an untested principle, appealing but mired with
unknowns and known obstractions
(Read: Risks & Opportunities Abound)
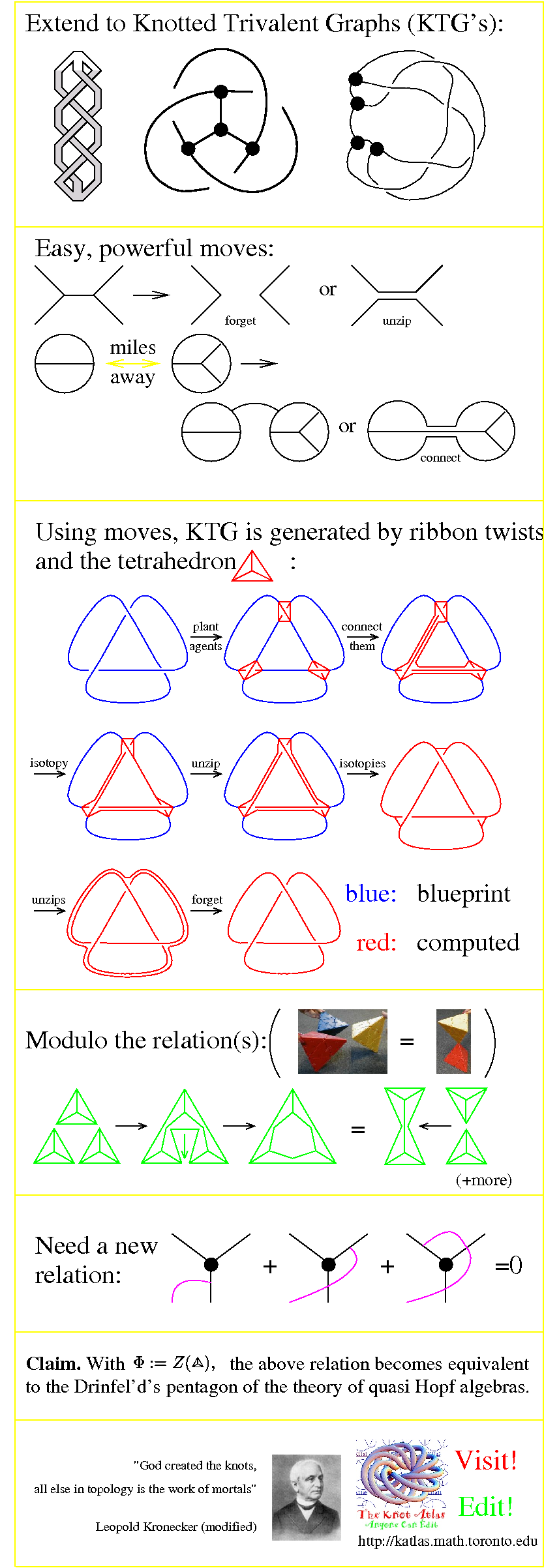
- The Thesis. Every 3D property of knots and link is definable in terms of Knotted
Trivalent Graphs.
- 3D Property.
-
Having braid index 6.
-
Having a projection with 23 crossings.
-
Having an alternating projection.
-
Bounding a disk in B4.
-
Being algebraic.
- Having unknotting number 3.
- Bounding a Seifert Surface of genus < 7.
- Being a boundary link.
- Being a ribbon knot.
- Being fibred.
- Having a vanishing Alexander polynomial.
- Definable. Within some given
collections of objects, in terms of a finite formula utilizing some
operations provided in advance. Examples:
- In algebra.
- In strict knot and link theory.
- Knotted Trivalent Graphs.
- The Principle. Seek a TG-morphism from
KTG to algebra.
- Aside. KTG is finitely presented - to find a TG-morphism
you need to make two guesses and carry out three checks. And when
you're done, you've rediscovered Drinfel'd's theory of associators.
- A Prime Candidate. The theory of finite
type invariants, as studied in Stonhenge.
- A Sad Truth. Z is practically surjective at
bounded degrees for several definable classes of knots (e.g. Ng's arXiv:q-alg/9502017).
There are also some bad news about "bounded loop counts"
(Garoufalidis-Rozansky arXiv:math.GT/0003187).
- Put Your Name Here.
- Do the Alexander test case - recover Fox-Milnor (for ribbon knots,
A(t)=f(t)f(1/t)).
- What's in the envelope of the Alexander polynomial, if we're talking
about knots or graphs?
- Control the Alexander associator (see Lieberum's arXiv:math.QA/0204346).
- Pull something out of Jones' envelope.
- Find the envelopes of other interesting finite type invariants.
- Study other internal quotients of the TG-algebra of chord diagrams.
There are plenty, even plenty with polynomial behaviour!
- Formalize and classify such internal quotients.
- Tame one associator and show it to your friends. (Or be brave and
master the theory of multiple ζ-numbers).
- Complete the Stonhenge story for KTGs.
- Venture outside of Stonehenge! Surgery quotients?
- Are fibred knots definable?
- Are there other interesting definable classes of knots?
- What's "a TG-algebra"? (See D. Thurston's arXiv:math.GT/0311458).
Make precise the sufficiency of the pentagon and the hexagons for KTG.
