Legend:
Input Joint. Output
Joint. Supporting
Joint. Active
Joint. |
|
|
|
Linkages as Functions
How versatile configuration spaces for linkages can be? In the last lesson, we have found configuration spaces represented by various surfaces. What are the possible surfaces that can represent configuration spaces? And in general, what are the possible manifolds with this property? A partial answer to this question was given by a proof of M. Kapovich and J. Millson[KM], as follows: For each smooth compact manifold, M there exists a linkage with configuration space homeomorphic to a finite number of copies of M. In this lesson we will explore the proof of this fact.
First, we introduce a new usage for linkages, as calculation devices: The calculations will be preformed on numbers in the complex plane. As a first example we construct a linkage, which can be used to calculate the translation of a point in the plane by a constant vector V:
| Legend:
Input Joint.Output
Joint.Supporting
Joint.Active
Joint. |
|
|
|
All along the motion of the above linkage, the red joint is translated by a constant vector from the green joint, since the linkage is composed of 2 parallelograms. We call the green joint the input joint and call the red joint the output joint. By selecting for example the vector (10,0) for the translation vector, one can compute the function Y = X+10 for a complex number X in a restricted area of the plane. Notice that by resizing the bars of the Translator Linkage we can compute translation in a large area of the complex plane as we would like.
Another useful linkage is the Pantograph, below. Its basic usage is to compute scalar products: Y = l·X
Scalar Multiplier for l>1 the anchor is placed at (0,0) |
l·AD = AF, l·EF = CF, |
As in the previous linkage, the Pantograph can only be used in a restricted area of the plane, but by resizing the bars, the restricted area could be as large as we would like.
In order to compute the function y = l·X for a<1 we switch the anchored joint as in the following applet:
|
|
| Scalar Multiplier for 0<l<1 | Scalar Multiplier for l<0 |
by loosening the only anchor of the Pantograph we can compute functions with 2 input joints (say B and C) of the form: output=C+(B-C)·l. By setting l=0.5 we can compute the average:
Next is the Inversor linkage which computes the function:
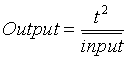t >0
 g·(g+2a) = a2 - b2 = t2 |
The only anchor is pinned at (0,0), the output joint equals the input joint on the circle of radius t around (0,0) .
The Inversor linkage is the base for the Peacullier's Linkage, a linkage that transforms radial motion into linear motion. We will use the Peacullier's Linkage in the next page.
Below is a linkage for the addition of 2 numbers which is constructed from 2 Pantographs:
The idea behind the construction of the Adder linkage is first to
interpret addition of two numbers as a composition of 'simpler functions'. In order to
calculate the value of y = A+B we first calculate c=(A+B)/2 and
finally we calculate y = 2·c. This concept easily transforms to the use of
linkages: we use 2 pantograph, the first with 2 input joints and scalar l = 0.5, which corresponds to the function (A+B)/2.
The second Pantograph with one anchor pinned at (0,0) and scalar l=2
, which corresponds to the function y=2·c. we identify the output joint
of the first Pantograph with the input joint of the second Pantograph to construct a
linkage for addition. Finally, in order for the linkage to work we must construct the
second Pantograph so its input domain will contain the output joint of the first
Pantograph. Since we can resize the Pantograph to include a large domain as we wish this
task is always possible. In the general case, we can construct linkages for complex
functions by composing the function to a series of 'simple functions' which we already
know how to construct a linkage for and sequentially identify output joints of input
joints. As an example, we will construct a linkage for multiplication in this way:
First we construct a linkage for the computation of the function y = x2,
by using the equation:
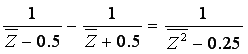
we can sequentially construct a linkage for squaring:
Combine a Translator linkages with parameters t = -0.5 and Inversor
linkage to produce the function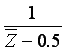 
, similar produce such a linkage for 
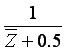by selecting a new Translator with t = 0.5 and a
new Inversor.
Compose the linkage for 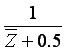and a pantograph with l = -1
to calculate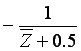 
Compose an adder linkage with 2 input joints as the output joints of the
linkages for 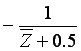and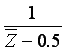
By attaching another Inversor Linkage to the output of the Adder we compute Z2-0.25.
Finally we attach a translator linkage with t = 0.25 to produce Z2.
Note that we can not compute the square for Z = ±0.5, Z = 0.25 with this specific linkage. However by using the equation:
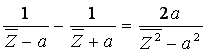
for a>1 and selecting the last Inversor Linkage with inversion radius t, such that t2 = 2a, we can compute W = Z2, for ||Z||<a .
And now for the Squaring Linkage
To construct a Multiplier Linkage for 2 numbers W, Z we use the equation :
![[(W+Z)^2-(Z^2+W^2)]/2=Z·W](images/comp5.gif)
to similarly compose the required linkage.
Since we know how to multiply ,translate by a constant , and add numbers we can compute any given polynomial function f(Z1,...,Zn) by sequentially composing linkages. By selecting a large enough input domain for each simple linkage in the sequence we can compute f on any restricted domain in the plane.
There is little practical use to functional linkages as calculation devices (as you have probably figured out by testing the Squaring Linkage), but in the next page, we will find the importance of them.
