For a compact symplectic manifold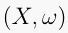 
, a Riemann-
Roch number 
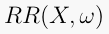is defined by
.
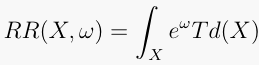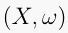is a prequantizable symplectic toric manifold, it is wellknown
that 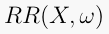can be computed by counting lattice points in
the image of the moment map. In this talk, we observe this relationship
for certain Lagrangian fibrations.
Let 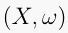be a 2n-dimensional closed, connected symplectic manifold
and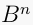 
an n-dimensional manifold with corners. A map 
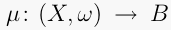is called a locally toric Lagragian fibration if 
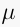is locally identified
with the map 
defined by
.
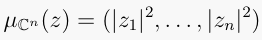For a locally toric Lagrangian fibration 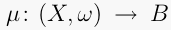, in general,
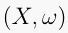no longer admits a global torus action, but locally it does. In
this talk, we investigate 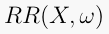in terms of the local torus actions
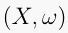in the case where is prequantizable. Under an appropriate condition,
we can generalize a moment map, and we see that the above
relationship still holds for some example.