For a compact symplectic manifold 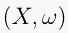 , a Riemann-
Roch number
, a Riemann-
Roch number  is defined by
is defined by
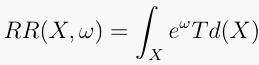 .
.
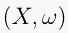 is a prequantizable symplectic toric manifold, it is wellknown
that
is a prequantizable symplectic toric manifold, it is wellknown
that  can be computed by counting lattice points in
the image of the moment map. In this talk, we observe this relationship
for certain Lagrangian fibrations.
Let
can be computed by counting lattice points in
the image of the moment map. In this talk, we observe this relationship
for certain Lagrangian fibrations.
Let 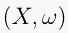 be a 2n-dimensional closed, connected symplectic manifold
and
be a 2n-dimensional closed, connected symplectic manifold
and 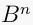 an n-dimensional manifold with corners. A map
an n-dimensional manifold with corners. A map  is called a locally toric Lagragian fibration if
is called a locally toric Lagragian fibration if 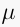 is locally identified
with the map
is locally identified
with the map 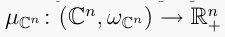 defined by
defined by
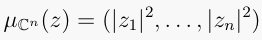 .
.
For a locally toric Lagrangian fibration  , in general,
, in general,
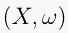 no longer admits a global torus action, but locally it does. In
this talk, we investigate
no longer admits a global torus action, but locally it does. In
this talk, we investigate  in terms of the local torus actions
in the case where
in terms of the local torus actions
in the case where 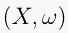 is prequantizable. Under an appropriate condition,
we can generalize a moment map, and we see that the above
relationship still holds for some example.
is prequantizable. Under an appropriate condition,
we can generalize a moment map, and we see that the above
relationship still holds for some example.