The Casimir connection of a simple Lie algebra g yields
a family of commuting quantum Hamiltonians acting on the
weight spaces of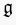 
-modules. I will explain how to diagonalise
these Hamiltonians by using the affine Kac--Moody algebra
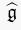at critical level. This mirrors the construction
of Feigin--Frenkel--Reshetikhin, who diagonalised the Gaudin
Hamiltonians arising from the Knizhnik--Zamolodchikov
connection, and leads to a new class of quantum integrable
systems generalizing the Gaudin model.
These integrable systems are quantisations of the shift of
argument algebras, that is the maximal Poisson commutative
subalgebras of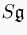 
introduced by Mishenko--Fomenko.
This is joint work with B. Feigin and E. Frenkel.