UNIVERSITY OF TORONTO

DEPARTMENT OF MATHEMATICS

MAT 237 Y - MULTIVARIABLE CALCULUS

FALL-WINTER 2005-06

TEST #3. MARCH 23, 2006.

1. (15 marks) Evaluate   where  E  is the solid tetrahedron bounded by the four planes

x = 0 ,  y = 0 ,  z = 0  and  6 x + 3 y + 2 z = 6 .

Soln.   =

=  =

=  = .

2. (15 marks) Evaluate    where  R  is the

parallelogram enclosed by the lines  y = x ,  y = x – 2 ,  x + 2 y = 1  and  x + 2 y = 4 .

Soln. We make  u = x – y  and  v = x + 2 y .

Then    and   .

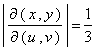Now,   =

=  =  .

3. (10 marks) Let  f  and  g  be any two functions of three variables such that both  f  and  g  are

differentiable and have continuous second-order partial derivatives. Show that  div ( Ñ f  ´ Ñ g ) = 0 .

Soln.  Ñ f  ´ Ñ g = (  f _x ,  f _y ,  f _z  ) ´ (  g _x , g _y , g _z  )

= (  f _y  g _z  –  f _z  g _y  ,  f _z  g _x  –  f _x  g _z  ,  f _x  g _y  –  f _y  g _x  )  and

div (Ñ f  ´ Ñ g ) =  f _{x y}  g _z  +  f _y  g _{x z}  –  f _{x z}  g _y  –  f _z  g _{x y}

+  f _{y z}  g _x  +  f _z  g _{x y}  –  f _{x y}  g _z  –  f _x  g _{y z}  + f _{x z}  g _y  +  f _x  g _{y z}  –  f _{y z}  g _x  –  f _y  g _{x z}

= 0 . 

4. (10 marks) Let  F ( x , y , z ) = ( y + e ^{– z} sin x ) i + x j + ( 1 + e ^{– z} cos x ) k  and  C  be the curve

given by the vector function  r ( t ) = ( t ² – t + p ) i + t ² j  + ( t ³ – 1 ) k ,  0 ≤ t ≤ 1 .

Evaluate the line integral   .

Soln. Notice that  F = Ñ f  , where  f ( x , y , z ) = x y – e  ^{– z} cos x + z .

Then   = f ( r ( 1 ) – r ( 0 ) ) = f ( p , 1 , 0 ) – f ( p , 0 , – 1 )

=  p + 1 – e + 1 = p + 2 – e .

5. (10 marks) Evaluate the line integral    where  C  is the

positively oriented triangle with vertices  ( 0 , 0 ) ,  ( 2 , 1 )  and  ( – 2 , 1 ) .

Soln. Using Green’s Theorem we obtain:

 =

=  =  =  = 4 ( e – 1 ) .

6. (15 marks) Compute the surface area of the torus represented parametrically by the coordinate functions

x = ( 3 + cos s ) cos t ,  y = ( 3 + cos s ) sin t  and  z = sin s , where  0 ≤ s ≤ 2 p  and  0 ≤ t ≤ 2 p  .

Soln.  r _s = ( – sin s cos t , – sin s sin t , cos s )  and  r _t = ( – ( 3 + cos s ) sin t , ( 3 + cos s ) cos t , 0 ) . 

Then,  r _s ´ r _t = – ( 3 + cos s ) ( cos s cos t , cos s sin t , sin s )  and  ½ r _s ´ r _t ½ = 3 + cos s .

Finally,  A =  =  = 12 p  ² .

7. (15 marks) Evaluate the surface integral   where  F ( x , y , z ) = 3 x i + y j + z k  and

S  is the hemisphere  x ² + y ² + z ² = 4 ,  z ³ 0 .

Soln. The given surface is the graph of the function    where  x ² + y ² ≤ 4 .

Then,   =  ,  where  W = { ( x , y ) ½ x ² + y ² ≤ 4 } .

That is,   =  . Now, using polar coordinates, we obtain:

 =

=  =  .

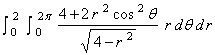
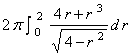Finally, we make  r = 2 sin w , then:

 =  =

=  = 80 p / 3 .

8. (10 marks) Show that for each pair of points  G  and  H  on the xy-plane, there exists a pair of

real constants  p  and  q  such that  = 0 , where  C  is

the line segment that joins  G  and  H .

Soln. Let  G = ( a , b )  and  H = ( c , d ) . Then, the line segment  C  can be parametrized as

x = a + ( c – a ) t  and  y = b + ( d – b ) t , where  0 ≤ t ≤ 1 .

Now,   =

If  a = c , then   = 0  for any choice of  p , otherwise,

 =  =

=  .

Thus, by taking  p = ( a + c ) / 2 , we obtain   = 0 .

Similarly, by taking  q = ( b + d ) / 2 , we obtain   = 0 .

So,  by taking  p  and  q  as the coordinates of the midpoint of the segment  GH  , we obtain,

= 0 .