UNIVERSITY OF TORONTO

DEPARTMENT OF MATHEMATICS

MAT 237 Y - MULTIVARIABLE CALCULUS

FALL-WINTER 2005-06

ASSIGNMENT #6. DUE ON MARCH 16, 2006.

1. a) Suppose that a thin wire is bent into the shape on the (unbounded) curve of intersection of the surfaces

x = 5 y ²  and  z = 7 y . Find the mass of the wire if its linear density at any point  ( x , y , z )  is given by the

function  d ( x , y , z ) = ( 1 + 2 y ² ) ^{– 3 / 2}  .

b) Evaluate the line integral    , where  C  is the curve

and  z = t ² , with  0 £ t £ 2 . Use your result to compute   .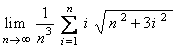

2. a) Let  F ( x , y , z ) = ( 2 x z + y e ^x + y ) i + ( e ^x + z e ^{y z} ) j + y e ^{y z} k  and  let  C  be the curve

x =  sin t ,  y =  2 cos t  and  z = sin ( 2 t ) , with  0 ≤ t ≤ 2 p . Compute  .

b) Let  F ( x , y , z ) =  i +  j +  k  and let  C

be the curve  x = t ,  y = e ^t ,  z = e ^{2 t} , with  0 ≤ t ≤ 1 . Show that  < 3 e ² .

3. a) Evaluate the surface integral    where  S  is the plane  x + 2 y + 2 z = 6 .

b) Suppose that  S  is a right-circular conical shell with uniform density. Let  h  denote its height and let  a  denote the radius of its base. What happens to the centre of mass of the surface  S  when the value of  a  increases if the value of  h  remains unchanged?

4. Show that the value of the line integral    does not depend on the parametrization of the curve  C .