UNIVERSITY OF TORONTO

DEPARTMENT OF MATHEMATICS

MAT 237 Y - MULTIVARIABLE CALCULUS

FALL-WINTER 2005-06

ASSIGNMENT #5. DUE ON FEBRUARY 16, 2006.

1.  Show whether each of these integrals converges or diverges and find the value if it      converges.

a) 

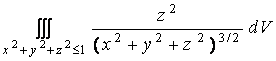
b)          

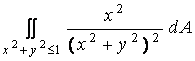
c)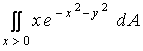           

2. a)  Let  S  be the region in the first quadrant bounded by

x y = 1 ,  x y = 3 ,  x ² – y ² = 1  and  x ² – y ² = 4 .

Find   .

b)  Let  S  be the region in the first quadrant bounded above by  x + y = 1 .

Find   .

Note that the function does not exist for the origin and explain how the integral can still be taken.

3. Let  B _n ( r ) = { x Î R ⁿ ï  ≤ r }  be the sphere of radius  r , centred at the origin.

Let    be the volume of the sphere.

a)  Show that   .

b)  Rewrite    as    for some bounds  f  and  g  and with

a  dependent on  x  and  y .

c)  Evaluate the integral above to find    in terms of   .

d)  Find a closed form for   .

4.  Let    and let  S  be the unit square.

a)  Show that   .

b)  Show that the iterated integrals for the function  f  exist, but are unequal.