UNIVERSITY OF TORONTO
DEPARTMENT OF MATHEMATICS
MAT 237 Y - MULTIVARIABLE CALCULUS
FALL-WINTER 2005-06
ASSIGNMENT #5. DUE ON FEBRUARY 16.
PROBLEMS
Do not submit your solutions without the cover page.
READ THE INSTRUCTIONS WRITTEN ON THAT PAGE.
1. Show whether each of these integrals converges or diverges and find the value if it converges.
a)
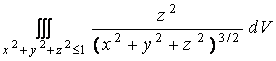
b)
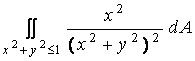
c)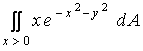 
2. a) Let S be the region in the first quadrant bounded by
x y = 1 , x y = 3 , x 2 – y 2 = 1 and x 2 – y 2 = 4 .
Find
.
b) Let S be the region in the first quadrant bounded above by x + y = 1 .
Find
.
Note that the function does not exist for the origin and explain how the integral can still be taken.
3. Let B n (
r ) = { x
Î
R n
ï
≤
r } be the sphere of radius r , centred at the origin.
Let 
be
the volume of the sphere.
a) Show that 
.
b) Rewrite
as
for
some bounds f and g and with
a dependent on x and y .
c) Evaluate the integral above
to find in
terms of 
.
d) Find a closed form for 
.
4. Let 
and
let S be the unit square.
a) Show that 
.
b) Show that the iterated integrals for the function f exist, but are unequal.
|
• HOME |