UNIVERSITY OF TORONTO
DEPARTMENT OF MATHEMATICS
MAT 237 Y - MULTIVARIABLE CALCULUS
FALL-WINTER 2005-06
ASSIGNMENT #3. SOLUTIONS
1.
a) Let u ( x 1 , x 2 ,
, x n ) =
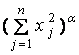 ,
where a
is a constant, and n is given.
,
where a
is a constant, and n is given.
Find all the values of the constant
a
, if any, for which the function u satisfies the partial
differential equation 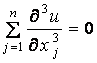 .
.
Solution:
Let w =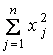 ,
then
,
then 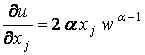 ,
,
 ,
and
,
and
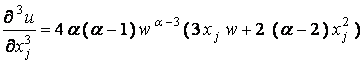 .
.
Therefore,
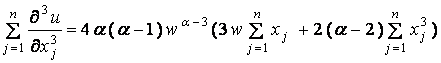 .
.
And this is 0 for any choice of ( x 1 , x 2 , , x n ) only when a = 0 or a = 1 .
(Except in the trivial case n = 1 , where a = 1 / 2 is also a solution.)
In effect, if a ¹ 0 and a ¹ 1, taking ( x 1 , x 2 , , x n ) = ( 1 , 0 , , 0 ) , we have
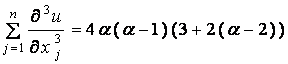 and a
= 1 / 2 is required.
and a
= 1 / 2 is required.
But taking now ( x 1 ,
x 2 ,
, x n ) = ( 1 , 1 , 0 ,
,
0 ) , we obtain,
 ,
which is ¹
0 when a
= 1 / 2 .
,
which is ¹
0 when a
= 1 / 2 .
b)
Let F : R 2
®
R be a function whose partial derivatives are continuous and suppose
that the equation F ( r cos
q
, z + r sin
q
) = 0 implicitly defines z as a function of the variables r
and q
. Find all the values of the constant
b
, if any, for which z satisfies the partial differential equation
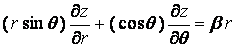 .
.
Solution:
 and
and 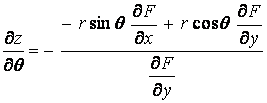 .
.
Then,
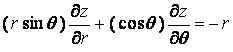 .
Therefore b
= 1 .
.
Therefore b
= 1 .
2. a)
Suppose that E is the
ellipsoid ![]() ,
where a > 0 , b > 0 and a
¹
b .
,
where a > 0 , b > 0 and a
¹
b .
Let d ( x , y , z ) denote the distance from the point ( 0 , 0 , 0 ) to the line that is normal to the ellipsoid E at the point ( x , y , z ) . Find the maximum value of the function d and determine all points ( x , y , z ) where this maximum value is reached.
Solution:
The given ellipsoid is a surface of revolution about the z-axis and is also symmetric with respect to the xy-plane . It means that the desired maximum is reached at a point ( x , y , z ) of the given ellipsoid if and only if it is also reached at any point ( x cos t , y sin t , ± z ) , where
0 £ t £ 2 p . So, it will be enough to find the unique solution to the problem for the case
y = 0 , x > 0 , z > 0 and then generalize to the whole family of solutions.
The resulting two-dimensional curve a 2 x 2 + b 2 z 2 = 1 , x > 0 , z > 0 can be parametrized as
![]() .
Then, the tangent line to the curve at any point ( x , z )
follows the direction of the vector
.
Then, the tangent line to the curve at any point ( x , z )
follows the direction of the vector
![]() .
The distance d from ( 0 , 0 ) to
.
The distance d from ( 0 , 0 ) to
the line L that passes through ( x , z ) and is perpendicular to the curve is then given by
d
=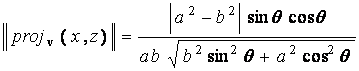 .
.
Now, d
¢
=  and
d
¢
= 0 only when a cos 2
q
b sin 2
q
= 0 .
and
d
¢
= 0 only when a cos 2
q
b sin 2
q
= 0 .
That is, tan
q
= ![]() ,
therefore x =
,
therefore x = 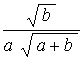 and
z =
and
z =  .
.
The maximum value for d
is 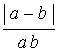 .
This maximum value is reached at any of the points
.
This maximum value is reached at any of the points
( x , y , z
) = 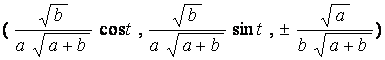 ,
where 0
£
t
£
2
p
.
,
where 0
£
t
£
2
p
.
b) A small insect is seating at the point ( 4 , 3 , 1 ) inside a cage in the shape of the hollow rectangular region 0 £ x £ 5 , 0 £ y £ 5 , 1 £ z £ 4 . Suppose that the temperature at any point ( x , y , z ) in the cage is given by the function T ( x , y , z ) = 30 + x 2 + 2 y 2 z 2 .
In order to cool off as soon as possible, the insect flies off from its position at the bottom of the cage in such a way that it experiences the maximum possible rate of cooling at each of the points of its trajectory. What are the coordinates of the point at which the insect reaches the top of the cage?
Solution:
Let r ( t ) = ( x ( t ) , y ( t ) , z ( t ) ) denote the position of the insect at time t , where t ³ 0 and r ( 0 ) = ( 4 , 3 , 1 ) . At any point ( x , y , z ) , the vector Ñ T ( x , y , z ) points in the direction of maximum decrease of the temperature. So, the condition required for the insects trajectory is r ¢ = l Ñ T , l > 0 .
Taking l = 1 , we obtain x ¢ ( t ) = 2 x ( t ) , y ¢ ( t ) = 4 y ( t ) and z ¢ ( t ) = 2 z ( t ) .
Then, x ( t ) = 4 e 2 t , y ( t ) = 3 e 4 t and z ( t ) = e 2 t . For z ( t ) = 4 , t = ln 2 .
The insect reaches the top of the cage at the point ( 1 , 3 / 16 , 4 ) .
3. a) Question 2-5 from Spivak:
Let f : R 2
®
R be defined by  .
.
Show that f is not differentiable at ( 0 , 0 ) .
Solution:
Notice that
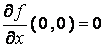 and
and
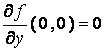 .
So, the function f is differentiable at ( 0 , 0 ) if and only if
.
So, the function f is differentiable at ( 0 , 0 ) if and only if
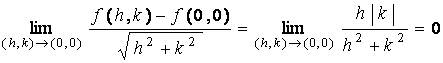 .
But taking h = k >0 , we obtain
.
But taking h = k >0 , we obtain
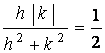 and
the limit as ( h , k )
®
( 0 , 0 ) can not be 0 .
and
the limit as ( h , k )
®
( 0 , 0 ) can not be 0 .
b) Define f , g : R
3 ®
R by ![]() and
and
![]() ,
where u , v , w : R 3
®
R are continuous functions, with continuous partial derivatives, and
such that for all (
x , y , z )
,
where u , v , w : R 3
®
R are continuous functions, with continuous partial derivatives, and
such that for all (
x , y , z )
u x ( x , y , z ) + v y ( x , y , z ) + w z ( x , y , z ) = 0 .
Show that f , g and w satisfy the partial differential equation f x + g y = w .
Solution:
Notice that f x
( x , y , z ) =
![]() and
and
g
y ( x
, y , z ) =
![]() .
Then,
.
Then,
f
x ( x
, y , z ) + g y ( x , y
, z ) =
![]()
=
![]() =
=![]() =
w
( x , y , z )
=
w
( x , y , z )
4. a) Question 2-24 from Spivak:
Define f : R 2
®
R by  .
.
a1) Show that f y ( x , 0 ) = x for all x and f x ( 0 , y ) = y for all y .
Solution:
f
y ( x , 0 ) =
 .
.
So, f y ( x , 0 ) = x for all x . Similarly,
f
x ( 0 , y ) =
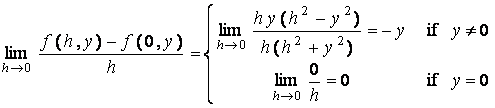 .
.
So, f x ( 0 , y
) = y for all y .
![]()
a2) Show that f x y ( 0 , 0 ) ¹ f y x ( 0 , 0 ) .
Solution:
f
x y ( 0 , 0 ) =
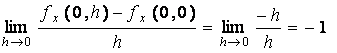 and
similarly f y x ( 0 , 0 ) = 1 .
and
similarly f y x ( 0 , 0 ) = 1 .
b) Question 2-32 from Spivak:
b1) Let f : R
®
R be defined by 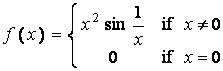 .
.
Show that f is differentiable at 0 but f ¢ is not continuous at 0 .
Solution:
f
¢
( 0 ) = 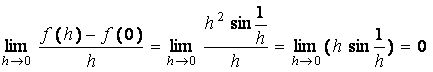 ,
because 1 £
,
because 1 £
![]() £
1 .
£
1 .
Now, if x
¹
0 , f ¢
( x ) = ![]() .
But
.
But ![]() does
not exist.
does
not exist.
So, f ¢ is not continuous at 0 .
b2) Let f : R 2
®
R be defined by 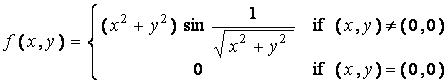 .
.
Show that f is differentiable at ( 0 , 0 ) but f x and f y are both discontinuous at ( 0 , 0 ) .
Solution:
As in (b1), it is easy to conclude that
f x ( 0 , 0 ) = 0 and f x (
x , 0 ) =![]() if x > 0 .
if x > 0 .
Similarly, f y ( 0
, 0 ) = 0 and f y ( 0 , y ) =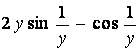 if y > 0 . Therefore, f x and f
y are both discontinuous at ( 0 , 0 ) .
if y > 0 . Therefore, f x and f
y are both discontinuous at ( 0 , 0 ) .
Now, with f x ( 0
, 0 ) = 0 = f y ( 0 , 0 ) , in order to show that
f is differentiable at ( 0 , 0 ) we only have to prove that
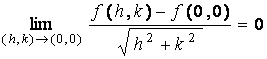 .
.
But
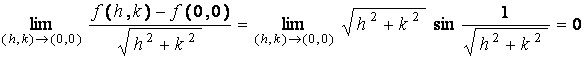 .
.
|
HOME |
|